 ={2, 4},
={2, 4},  ={2, 3, 5},
={2, 3, 5}, 
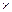
 ={<2, 2>,<2, 3>,<2, 5>,<4, 2>,<4, 3>,<4, 5>},
={<2, 2>,<2, 3>,<2, 5>,<4, 2>,<4, 3>,<4, 5>},
R = {<2, 2 >, <2, 3>, <2, 5>}.
Дополнением бинарного отношения R между множествами  и
и  называется множество – R = (
называется множество – R = (
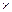
 )\ R. Обратным отношением для R называется R –1 = {<
)\ R. Обратным отношением для R называется R –1 = {<  , y >: < y,
, y >: < y,  > Î R }. Образом множества Х относительно R называется множество R (X) = { y:
> Î R }. Образом множества Х относительно R называется множество R (X) = { y: 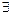
 Î X: <
Î X: <  , y > Î R }.
, y > Î R }.
Здесь R Í 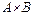 , X Í
, X Í  , R (X)Í
, R (X)Í  . Прообразом Y относительно R называется R –1(Y).
. Прообразом Y относительно R называется R –1(Y).
Композицией бинарных отношений R1 Í 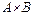 и R2 Í B
и R2 Í B 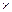 C называется множество
C называется множество 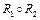 = {<
= {<  , z >:
, z >: 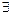 y: <
y: <  , y > Î R1, < y, z > Î R2 }.
, y > Î R1, < y, z > Î R2 }.
Свойства бинарных отношений:
1) (R –1)–1 = R;
2) (R1 È R2)–1 = R1 –1 È R2 –1;
3) (R1 Ç R2)–1 = R1 –1 Ç R2 –1;
4) –(R –1) = (– R)–l;
5) 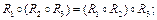
6) (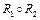 )–1 =
)–1 = 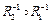 ;
;
7) 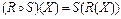 ;
;
8) 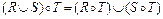 ;
;
9) 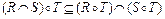 .
.
Замечание к свойству 9. Обратное не всегда верно. Пример:
 = {
= {  },
}, 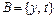 ,
, 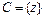 , R = {<
, R = {< 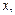 y >}Í
y >}Í  ´
´  , S ={<
, S ={< 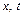 >}Ì A ´ C,
>}Ì A ´ C, 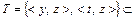
 ´ C, R Ç S =
´ C, R Ç S = 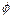 Þ (R Ç S)
Þ (R Ç S) 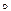 T =
T = 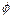 , R
, R 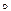 T ={<
T ={< 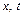 >}, S
>}, S 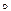 T = {<
T = {< 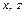 >} Þ (R
>} Þ (R 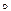 T) Ç (S
T) Ç (S 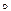 T) = {<
T) = {< 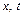 >}.
>}.
 2015-06-28
2015-06-28 408
408








