Эквивалентность

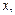
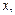
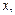
Бинарное отношение i_A ={< >: Î } называется диагональю. Бинарное отношение R на называется рефлексивным, если " Î : < >Î R; иррефлексивным, если " Î : < >Ï R; симметричным, если < 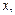y >Î R Þ < y, >Î R; антисимметричным, если 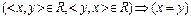; транзитивным, если 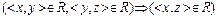. Рефлексивное, симметричное, транзитивное бинарное отношение на называется эквивалентным. Классом эквивалентности элемента по эквивалентности R называется / R = { у: < 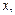y >Î R }.

Пример. М = {1; 2; 3; 4; 5}, R = {(1; 1), (1; 2), (2; 1), (2; 2), (3; 3), (4; 4), (5; 5)}. Является ли бинарное отношение R рефлексивным, симметричным, транзитивным, иррефлексивным, антисимметричным?

¨ Все пары (1; 1), (2; 2), (3; 3), (4; 4), (5; 5) принадлежат R, поэтому R рефлексивно. Пары (1; 2) и (2; 1) входят в R, все остальные пары симметричны. Это означает, что R симметрично. Все тройки пар, в которых третья получается “склеиванием” первых двух, входят в R одновременно. Это такие тройки пар: {(1; 1), (1; 2), (1; 2)}, {(1; 2), (2; 1), (1; 1)}, {(1; 2), (2; 2), (1; 2)}. Следовательно, R транзитивно. Пара (1; 1) принадлежит R, поэтому R неиррефлексивно. Для двух разных элементов 1 и 2 обе пары (1; 2) и (2; 1) входят в R, т. е. R неантисимметрично.

ТЕОРЕМА. Множество распадается на классы эквивалентности элементов множества по эквивалентности R.

Доказательство. (z Î / R) Þ ( / R = z / R). Действительно, по условию < 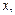z >Î R. Если t Î z / R, то < z, t >Î R. Отсюда < , t >Î R Þ t Î / R Þ z / R Í / R. Если t Î / R и z Î / R, то < 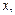t >Î R, < 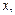z >Î R Þ < z, t >Î R Þ t Î z / R Þ x / R Î z / R. Из включений z / R Í / R Í z / R и следует искомое равенство.

Пусть z Î x / R Ç y / R. Тогда z Î / R, z Î y / R Þ / R = z / R = y / R Þ / R = y / R. Итак, два класса эквивалентности либо не пересекаются, либо совпадают. Так как < 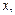>Î R, то Î / R и, следовательно, каждый элемент множества попадает в один из классов эквивалентности. Тем самым доказано, что множество – это объединение непересекающихся классов эквивалентности. ■