Декартовым (прямым) произведением множеств 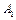 ,...,
,...,  n называется множество всех упорядоченных наборов элементов из
n называется множество всех упорядоченных наборов элементов из 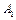 ,...,
,...,  n
n
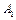 ´ ... ´ Аn= {< a1 ... an >: a1 Î A1,..., an Î An },
´ ... ´ Аn= {< a1 ... an >: a1 Î A1,..., an Î An },
гдe <a1...an>=<b1...bn> Û a1=b1 ... an=bn. Если 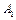 =…= Аn = А, то
=…= Аn = А, то 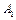 ´ ... ´ Аn называется декартовой степенью множества
´ ... ´ Аn называется декартовой степенью множества  и обозначается
и обозначается 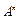 .
.
Свойства декартова произведения:
1) $ A, B, что 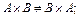
2) $ A, B, C, что 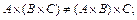
3) 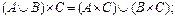
4) 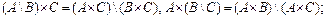
5) 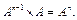
Примеры: [ а, в ] 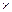 [ с, d ] – прямоугольник,
[ с, d ] – прямоугольник, 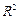 – плоскость, R 3 – трехмерное пространство.
– плоскость, R 3 – трехмерное пространство.
Подмножество R декартового произведения множеств А1,...,Аn называется п-местным отношением на множествах А1,...,Аn. Если R Í Xn, то имеем п -местное отношение на X.
 2015-06-28
2015-06-28 289
289








