Областью определения бинарного отношения R называется
dR = {  :
: 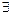 y: <
y: < 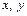 >Î R }.
>Î R }.
Областью значений бинарного отношения R называется множество
rR = { y: 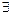 x: <
x: < 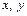 >Î R }.
>Î R }.
Бинарное отношение f Î  ´ В называется функцией из
´ В называется функцией из  в
в  , если
, если
1) df =  , rf Í
, rf Í 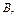
2) "  Î
Î  : (<
: (<  , y1 > = <
, y1 > = <  , у2 >) Þ (у1 = у2 ). т.е. для каждого элемента
, у2 >) Þ (у1 = у2 ). т.е. для каждого элемента  из
из  найдется не более одного элемента у Î В такого, что <
найдется не более одного элемента у Î В такого, что <  , у >Î f. Если rf =
, у >Î f. Если rf =  , то f – функция из
, то f – функция из  на
на 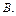 Вместо <
Вместо < 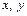 >Î f пишут у = f (
>Î f пишут у = f ( ), f:
), f:  ®
®  , при этом х называют аргументом, а у – значением функции f в точке
, при этом х называют аргументом, а у – значением функции f в точке  . Функция f называется инъекцией
. Функция f называется инъекцией  в
в  , если из того, что
, если из того, что 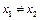 , следует, что
, следует, что 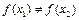 . Если rf =
. Если rf =  , то f называется сюръекцией
, то f называется сюръекцией  на
на  . Если f – инъекция и сюръекция одновременно, то говорят, что f осуществляет взаимнооднозначное соответствие между
. Если f – инъекция и сюръекция одновременно, то говорят, что f осуществляет взаимнооднозначное соответствие между  и В (биекция). Подстановкой множества
и В (биекция). Подстановкой множества  называется взаимнооднозначное отображение
называется взаимнооднозначное отображение  на себя. Множество всех функций из
на себя. Множество всех функций из  в
в  обозначается
обозначается 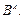 Если в определении функции множество
Если в определении функции множество  заменить на декартово произведение А1 ´ ... ´ Аn, то получим определение п-местной функции.
заменить на декартово произведение А1 ´ ... ´ Аn, то получим определение п-местной функции.
 2015-06-28
2015-06-28 332
332








