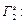Результатом подстановки вместо ребра 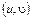 сети Г 1
сети Г 1 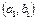 другой сети
другой сети 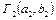 называется сеть, полученная удалением из сети Г 1
называется сеть, полученная удалением из сети Г 1 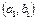 ребра
ребра 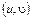 и отождествлением полюсов а 2,
и отождествлением полюсов а 2, 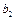 сети
сети 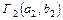 с вершинами
с вершинами 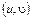 сети Г 1. Предположим, что сети Г 1
сети Г 1. Предположим, что сети Г 1 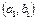 и
и 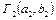 не пересекаются. Сеть Г 1
не пересекаются. Сеть Г 1 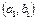 в этом случае называем внешней, а сети, которые подставляем в неё вместо рёбер, называем внутренними. Сеть Г (а,
в этом случае называем внешней, а сети, которые подставляем в неё вместо рёбер, называем внутренними. Сеть Г (а, 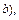 полученная из сетей, изоморфных сетям Г 1
полученная из сетей, изоморфных сетям Г 1 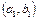 , …,
, …, 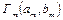 , путём применения конечного числа подстановок, называется суперпозицией этих сетей. Легко видеть, что суперпозиция – ассоциативная операция.
, путём применения конечного числа подстановок, называется суперпозицией этих сетей. Легко видеть, что суперпозиция – ассоциативная операция.
 Сеть a b называется тривиальной. Сильносвязная сеть называется разложимой, если её можно представить в виде суперпозиции нетривиальных непересекающихся сетей. В противном случае сеть называется неразложимой. На рис. 5.20 и 5.21 представлены примеры неразложимых сетей (полюса помечены кружочками).
Сеть a b называется тривиальной. Сильносвязная сеть называется разложимой, если её можно представить в виде суперпозиции нетривиальных непересекающихся сетей. В противном случае сеть называется неразложимой. На рис. 5.20 и 5.21 представлены примеры неразложимых сетей (полюса помечены кружочками).




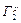 : : 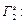
| |























| | | | | | | | | | | | | | | | |
| | | 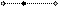 |
| | | |  |
| | | |  | |  |
| |
| |
| | |  | |  | |  |
| |
| | | Рис. 5.20 Рис. 5.21 Рис. 5.22 Рис. 5.23 Рис. 5.24
| |
Можно показать, что любая нетривиальная неразложимая сильносвязная сеть, имеющая не более шести рёбер, изоморфна одной из этих трёх сетей, т.е. не существует неразложимых сильносвязных сетей с тремя, четырьмя и шестью рёбрами. В то же время для каждого 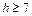 существуют неразложимые сильносвязные сети h с рёбрами. Это видно на рис. 5.23 и 5.24. Множество нетривиальных неразложимых сетей, отличных от
существуют неразложимые сильносвязные сети h с рёбрами. Это видно на рис. 5.23 и 5.24. Множество нетривиальных неразложимых сетей, отличных от 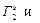
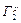 , обозначим через H и сеть, принадлежащую H, будем называть H -сетью.
, обозначим через H и сеть, принадлежащую H, будем называть H -сетью.
Пусть 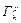 – сеть, представляющая собой параллельное соединение h рёбер,
– сеть, представляющая собой параллельное соединение h рёбер, 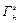 – последовательное соединение h рёбер,
– последовательное соединение h рёбер, 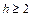 . Если сеть Г (а,
. Если сеть Г (а, 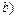 – суперпозиция сетей с внешней сетью
– суперпозиция сетей с внешней сетью 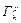 , то она называется p-разложимой. Если сеть – суперпозиция сетей с внешней сетью
, то она называется p-разложимой. Если сеть – суперпозиция сетей с внешней сетью 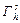 , то она называется s-разложимой. Если сеть – суперпозиция сетей с внешней H- сетью, то она называется H-разложимой. Подсеть называется сквозной, если её полюса – это полюса основной сети.
, то она называется s-разложимой. Если сеть – суперпозиция сетей с внешней H- сетью, то она называется H-разложимой. Подсеть называется сквозной, если её полюса – это полюса основной сети.
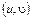 сети Г 1
сети Г 1 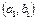 другой сети
другой сети 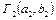 называется сеть, полученная удалением из сети Г 1
называется сеть, полученная удалением из сети Г 1 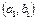 ребра
ребра 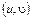 и отождествлением полюсов а 2,
и отождествлением полюсов а 2, 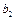 сети
сети 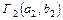 с вершинами
с вершинами 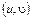 сети Г 1. Предположим, что сети Г 1
сети Г 1. Предположим, что сети Г 1 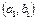 и
и 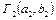 не пересекаются. Сеть Г 1
не пересекаются. Сеть Г 1 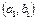 в этом случае называем внешней, а сети, которые подставляем в неё вместо рёбер, называем внутренними. Сеть Г (а,
в этом случае называем внешней, а сети, которые подставляем в неё вместо рёбер, называем внутренними. Сеть Г (а, 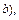 полученная из сетей, изоморфных сетям Г 1
полученная из сетей, изоморфных сетям Г 1 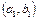 , …,
, …, 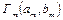 , путём применения конечного числа подстановок, называется суперпозицией этих сетей. Легко видеть, что суперпозиция – ассоциативная операция.
, путём применения конечного числа подстановок, называется суперпозицией этих сетей. Легко видеть, что суперпозиция – ассоциативная операция. Сеть a b называется тривиальной. Сильносвязная сеть называется разложимой, если её можно представить в виде суперпозиции нетривиальных непересекающихся сетей. В противном случае сеть называется неразложимой. На рис. 5.20 и 5.21 представлены примеры неразложимых сетей (полюса помечены кружочками).
Сеть a b называется тривиальной. Сильносвязная сеть называется разложимой, если её можно представить в виде суперпозиции нетривиальных непересекающихся сетей. В противном случае сеть называется неразложимой. На рис. 5.20 и 5.21 представлены примеры неразложимых сетей (полюса помечены кружочками).













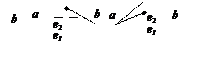
















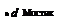
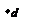
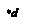
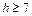 существуют неразложимые сильносвязные сети h с рёбрами. Это видно на рис. 5.23 и 5.24. Множество нетривиальных неразложимых сетей, отличных от
существуют неразложимые сильносвязные сети h с рёбрами. Это видно на рис. 5.23 и 5.24. Множество нетривиальных неразложимых сетей, отличных от 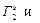
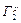 , обозначим через H и сеть, принадлежащую H, будем называть H -сетью.
, обозначим через H и сеть, принадлежащую H, будем называть H -сетью.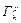 – сеть, представляющая собой параллельное соединение h рёбер,
– сеть, представляющая собой параллельное соединение h рёбер, 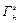 – последовательное соединение h рёбер,
– последовательное соединение h рёбер, 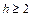 . Если сеть Г (а,
. Если сеть Г (а, 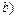 – суперпозиция сетей с внешней сетью
– суперпозиция сетей с внешней сетью 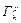 , то она называется p-разложимой. Если сеть – суперпозиция сетей с внешней сетью
, то она называется p-разложимой. Если сеть – суперпозиция сетей с внешней сетью 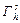 , то она называется s-разложимой. Если сеть – суперпозиция сетей с внешней H- сетью, то она называется H-разложимой. Подсеть называется сквозной, если её полюса – это полюса основной сети.
, то она называется s-разложимой. Если сеть – суперпозиция сетей с внешней H- сетью, то она называется H-разложимой. Подсеть называется сквозной, если её полюса – это полюса основной сети. 2015-06-28
2015-06-28 682
682