Граф с выделенными вершинами называется сетью. Выделенные вершины называются полюсами сети. Примером однополюсной сети является корневое дерево. Дерево с выделенной вершиной называется корневым деревом, а выделенная вершина называется корнем. Все вершины корневого дерева в зависимости от расстояния от корня обычно располагают по ярусам. Приведём индуктивное определение корневого дерева.
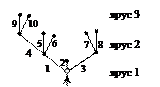 Базис индукции. Фигура рис. 5.15 является корневым деревом с корнем а.
Базис индукции. Фигура рис. 5.15 является корневым деревом с корнем а.
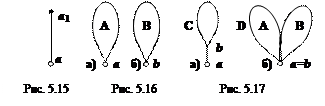
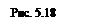
Гипотеза индукции. Пусть  – дерево с корнем а, В – дерево с корнем b (рис. 5.16).
– дерево с корнем а, В – дерево с корнем b (рис. 5.16).
Индуктивный переход. Тогда фигура С, полученная подключением к корню нового ребра (рис. 5.17а), тоже дерево. Фигура D, полученная из  и
и  отождествлением их корней, – тоже дерево (рис. 5.17б). Других деревьев нет.
отождествлением их корней, – тоже дерево (рис. 5.17б). Других деревьев нет.
Плоскую геометрическую реализацию дерева, в которой рёбра представляют отрезки прямых, а корень изображён вершиной со стрелкой, будем называть укладкой дерева. Стрелка указывает на то, что плоское корневое дерево изображается на плоскости с разрезом, представляющим собой полупрямую, исходящую из корня. Тем самым можно считать заданным направление подсчёта рёбер в ярусах слева направо.
Каждому плоскому корневому дереву с h рёбрами можно однозначно сопоставитьдвоичный вектор длины 2 h, называемый кодом дерева. Дереву с одним ребром сопоставим вектор 01. Если деревьям  и
и  (рис. 5.16) сопоставлены коды
(рис. 5.16) сопоставлены коды 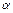 и
и 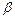 , то дереву С, полученному подключением ребра, – код 0
, то дереву С, полученному подключением ребра, – код 0 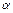 1, дереву D, полученному отождествлением корней, – код
1, дереву D, полученному отождествлением корней, – код 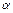
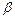 .
.
Каждой укладке дерева соответствует вектор-кортеж, содержащий поровну нулей и единиц, причём в любом его начальном отрезке нулей не меньше, чем единиц. Если в каком-либо собственном начальном отрезке кортежа нулей и единиц поровну, то это означает, что кортеж соответствует укладке дерева D, полученного из деревьев  и
и  отождествлением корней. Отсюда видно, что в силу индуктивности определения деревьев и кодов по своему кортежу укладка дерева восстанавливается однозначно, т.е. имеем взаимнооднозначное соответствие между укладками деревьев с h рёбрами и подмножеством множества кортежейдлины 2 h, содержащих поровну нулей и единиц. Обозначим через
отождествлением корней. Отсюда видно, что в силу индуктивности определения деревьев и кодов по своему кортежу укладка дерева восстанавливается однозначно, т.е. имеем взаимнооднозначное соответствие между укладками деревьев с h рёбрами и подмножеством множества кортежейдлины 2 h, содержащих поровну нулей и единиц. Обозначим через 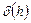 число всех попарно неизоморфных деревьев с h рёбрами, а через
число всех попарно неизоморфных деревьев с h рёбрами, а через 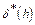 число всех различных укладок деревьев с h рёбрами.
число всех различных укладок деревьев с h рёбрами.
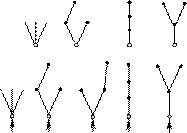 Пример. Все корневые деревья с тремя ребрами:
Пример. Все корневые деревья с тремя ребрами:
Все укладки с тремя ребрами:
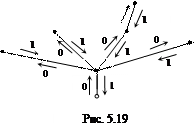
Задача. По заданному коду 001010011011 построить плоское корневое дерево.
Решение. Двигаемся от корня каждый раз по новому ребру, если в коде встретится 0, вправо от уже построенных рёбер, и возвращаясь по ребру, в случае, если в коде встретили 1.
ТЕОРЕМА.  <
< 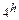 .
.
Доказательство. Число укладок равно числу кодов длины 2 h, поэтому 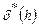 меньше числа кортежей длины 2 h из нулей и единиц, в которых нулей и единиц поровну, а оно меньше числа размещений с повторениями из 2 по 2 h. Отсюда
меньше числа кортежей длины 2 h из нулей и единиц, в которых нулей и единиц поровну, а оно меньше числа размещений с повторениями из 2 по 2 h. Отсюда
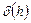 <
< 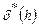 <
< 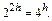 <
<
 2015-06-28
2015-06-28 4575
4575








