Граф без циклов называется лесом. Связный граф, не содержащий простых циклов, называется деревом.
ТЕОРЕМА. Граф является деревом Û любые две его различные вершины соединяет единственная цепь.
Доказательство очевидно.
ТЕОРЕМА. Связный граф является деревом 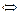 число вершин в нём на единицу больше числа рёбер.
число вершин в нём на единицу больше числа рёбер.
Доказательство. 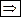 Пусть граф является деревом. Проведём индукцию по числу рёбер h. Если h = 1, то граф является деревом и у него число вершин на 1 превосходит число рёбер. Пусть для дерева с h = k рёбрами утверждение верно. Дерево, содержащее две или более вершин, имеет по крайней мере две концевые вершины. В самом деле, ими являются вершины маршрута максимальной длины в графе. После удаления из дерева одной из его концевых вершин вместе с инцидентным ей ребром вновь получается дерево. Рассмотрим дерево с k + 1 ребром. Удаление концевого ребра даёт нам дерево, удовлетворяющее гипотезе индукции. Так как удаление концевого ребра происходит с одновременным удалением и вершины, то в графе с k + 1 ребром наблюдается то же соотношение между числом рёбер и числом вершин, что и в графе с k рёбрами.
Пусть граф является деревом. Проведём индукцию по числу рёбер h. Если h = 1, то граф является деревом и у него число вершин на 1 превосходит число рёбер. Пусть для дерева с h = k рёбрами утверждение верно. Дерево, содержащее две или более вершин, имеет по крайней мере две концевые вершины. В самом деле, ими являются вершины маршрута максимальной длины в графе. После удаления из дерева одной из его концевых вершин вместе с инцидентным ей ребром вновь получается дерево. Рассмотрим дерево с k + 1 ребром. Удаление концевого ребра даёт нам дерево, удовлетворяющее гипотезе индукции. Так как удаление концевого ребра происходит с одновременным удалением и вершины, то в графе с k + 1 ребром наблюдается то же соотношение между числом рёбер и числом вершин, что и в графе с k рёбрами.
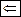 Пусть в связном графе n вершин и h рёбер, причём n = h + 1. Если в графе есть циклы, то из каждого цикла удаляем по одному ребру. В результате получим остовное дерево, в котором число вершин n, а рёбер
Пусть в связном графе n вершин и h рёбер, причём n = h + 1. Если в графе есть циклы, то из каждого цикла удаляем по одному ребру. В результате получим остовное дерево, в котором число вершин n, а рёбер 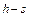 , где s – число удалённых рёбер. Из необходимой части теоремы
, где s – число удалённых рёбер. Из необходимой части теоремы 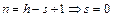 , т.е. исходный граф не имеет циклов.
, т.е. исходный граф не имеет циклов.
Число 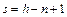 называется цикломатическим числом связного графа с n вершинами и h рёбрами.
называется цикломатическим числом связного графа с n вершинами и h рёбрами.
Следствие. Связный граф является деревом 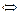 его цикломатическое число равно нулю.
его цикломатическое число равно нулю.
 2015-06-28
2015-06-28 921
921








