Пусть даны алфавиты Â = 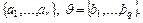 Обозначим через S (Â) и S (
Обозначим через S (Â) и S (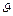 ) множества всех непустых слов в этих алфавитах. Соответствие между буквами алфавита Â и некоторыми словами в алфавите
) множества всех непустых слов в этих алфавитах. Соответствие между буквами алфавита Â и некоторыми словами в алфавите 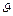 :
:
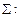 а 1 —
а 1 — 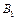
а 2 — 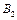
… … …
аr — 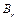
называют схемой. Тогда каждому слову 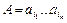 ставится в соответствие слово
ставится в соответствие слово 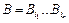 – код слова
– код слова  . Слова
. Слова 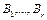 называются элементарными кодами. В случае, если из текста ясно, о какой схеме идёт речь, то мы будем говорить: Код
называются элементарными кодами. В случае, если из текста ясно, о какой схеме идёт речь, то мы будем говорить: Код 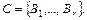 Если соответствие между словами
Если соответствие между словами  и их кодами взаимнооднозначное, то возможно декодирование, т.е. восстановление по коду исходного сообщения
и их кодами взаимнооднозначное, то возможно декодирование, т.е. восстановление по коду исходного сообщения 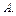 В этом случае говорят, что алфавитное кодирование является взаимнооднозначным, однозначно декодируемым или разделимым. Возникает вопрос: возможно ли по схеме å узнать, обладает ли она свойством взаимной однозначности?
В этом случае говорят, что алфавитное кодирование является взаимнооднозначным, однозначно декодируемым или разделимым. Возникает вопрос: возможно ли по схеме å узнать, обладает ли она свойством взаимной однозначности?
Пусть слово В имеет 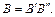 Тогда слово
Тогда слово 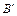 называется началом или префиксом слова В, а слово
называется началом или префиксом слова В, а слово 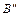 – концом или суффиксом слова В. При этом пустое слово Λ и само слово В считаются началами. Все начала и концы слова В, отличные от В и Λ, называются, собственными. Схема å обладает свойствам префикса (задаёт префиксный код), если никакой элементарный код не является префиксом другого элементарного кода.
– концом или суффиксом слова В. При этом пустое слово Λ и само слово В считаются началами. Все начала и концы слова В, отличные от В и Λ, называются, собственными. Схема å обладает свойствам префикса (задаёт префиксный код), если никакой элементарный код не является префиксом другого элементарного кода.
ТЕОРЕМА 1. Если схема å обладает свойством префикса, то алфавитное кодирование взаимнооднозначное.
Доказательство. По условию 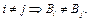 Предположим, что некоторое слово В допускает две расшифровки, т.е.
Предположим, что некоторое слово В допускает две расшифровки, т.е.
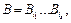
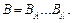
Следовательно,
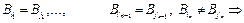 одно из слов
одно из слов 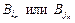 (то, которое короче) является префиксом другого. Противоречие. ■
(то, которое короче) является префиксом другого. Противоречие. ■
Обозначим через 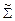 схему вида
схему вида 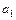 —
— 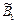
… …
аr — 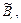 где
где
слово 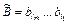 получено из слова
получено из слова 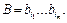 Тогда
Тогда 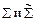 обладают свойством префикса и поэтому алфавитное кодирование взаимнооднозначное.
обладают свойством префикса и поэтому алфавитное кодирование взаимнооднозначное.
 2015-06-28
2015-06-28 1114
1114








