Самокорректирующиеся коды

Пусть В = {0; 1}. Рассматриваем единичный n -мерный куб Bⁿ как метрическое пространство, в котором для точек 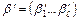и 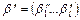расстояние 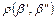определено по формуле 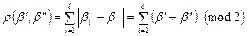(расстояние Хэмминга), т.е. это число координат, в которых различаются наборы 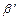и 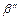. Обозначим через 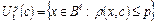шар радиуса p с центром c. Множество С кодовых слов будем коротко называть кодом С. Код C обнаруживает p ошибок, если ни одно кодовое слово не принадлежит шару радиуса p с центром в другом кодовом слове. Код исправляет p ошибок, если любые два шара радиуса p с центрами в кодовых словах не пересекаются.

ТЕОРЕМА. Код 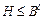исправляет p ошибок, 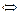расстояние между двумя любыми кодовыми словами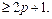

Доказательство. Условие 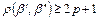эквивалентно тому, что шары 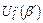и 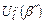с центрами в 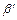и 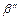радиуса p, не пресекаются. Если код исправляет p ошибок, то шары не пересекаются, ибо для точек пересечения неясно, в каком из слов 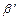или 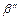допущены ошибки. Если шары не пересекаются, то любому слову из шара 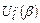ставится в соответствие единственная точка 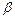, т.е. код исправляет любые p ошибки. ■

Упражнения

1. Для того, чтобы код обнаружил p ошибок, необходимо и достаточно, чтобы расстояние между любыми двумя кодовыми словами было 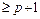. Докажите это.

2. Булева функция 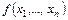называется характеристической функцией двоичного кода С, если она принимает значение 1 на С и 0 вне С. Сколько ошибок обнаруживает и исправляет код с характеристической функцией а) х ₁ Å … Å х_n; б) х ₁ … х_n Ú х ₁ … х_n?