Код Хэмминга исправляет одну ошибку, т.е. относится к классу самокорректирующихся кодов. В алфавите 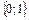 записываются все сообщения в виде слов длины m. Эти сообщения кодируются двоичными наборами
записываются все сообщения в виде слов длины m. Эти сообщения кодируются двоичными наборами 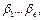 где
где 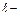 длина кода,
длина кода, 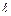 > m. Пусть
> m. Пусть 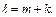 Предположим, что при прохождении кодового слова через канал связи произошла одна ошибка, в таком случае код сообщения на выходе может иметь вид:
Предположим, что при прохождении кодового слова через канал связи произошла одна ошибка, в таком случае код сообщения на выходе может иметь вид:
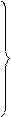
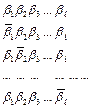
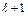 вариант.
вариант.
Для того, чтобы дополнительных разрядов в коде 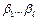 хватало для кодировки
хватало для кодировки 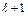 варианта, необходимо,
варианта, необходимо, 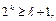 т.е.
т.е. 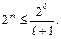 Выберём
Выберём 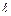 как наименьшее целое число, удовлетворяющее неравенству
как наименьшее целое число, удовлетворяющее неравенству 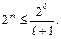
Алгоритм кодирования. Пусть 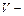 натуральное число
натуральное число 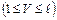 ,
, 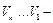 его двоичная запись. Построим последовательности:
его двоичная запись. Построим последовательности:
П0 = 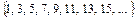 все числа с
все числа с 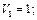
П1 = 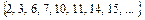 все числа с
все числа с 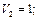
П2 = 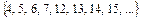 все числа с
все числа с 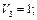
П3 = 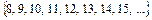 все числа с
все числа с 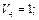
… … … … … … … … … …
Пк-1 = 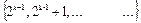 все числа с
все числа с 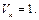
Члены 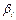 набора
набора 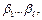 у которых i Î{1, 2, 4, …,
у которых i Î{1, 2, 4, …, 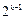 }, называют контрольными, а остальные – информационными. Слово
}, называют контрольными, а остальные – информационными. Слово 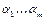 кодируется словом
кодируется словом 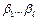 так:
так:
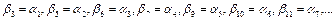
Затем определяются контрольные члены:
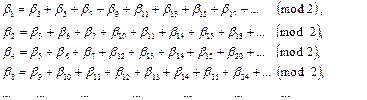
Обнаружение ошибки в кодах Хэмминга. Пусть при передаче кода 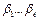 произошла ошибка в S- м члене, т.е. на выходе принято слово
произошла ошибка в S- м члене, т.е. на выходе принято слово 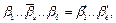 и пусть
и пусть 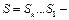 запись S в двоичном исчислении. Рассмотрим число
запись S в двоичном исчислении. Рассмотрим число 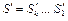 , где
, где
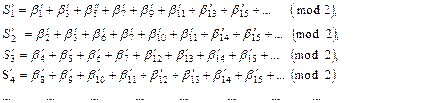 Тогда
Тогда 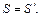 В самом деле, если
В самом деле, если 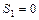 , то S не принадлежит первой последовательности и для
, то S не принадлежит первой последовательности и для 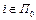 имеем
имеем 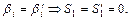 Если
Если 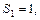 то S принадлежит последовательности П0
то S принадлежит последовательности П0 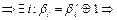
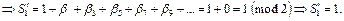 Следовательно, для обнаружения и исправления ошибки достаточно построить
Следовательно, для обнаружения и исправления ошибки достаточно построить 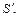
Декодирование. Требуется по коду 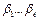 построить слово
построить слово 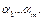 Для этого достаточно взять информационные члены в
Для этого достаточно взять информационные члены в 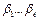 .
.
Пример 1. Закодировать по Хэммингу слово (111011100).
Решение. Заполнив информационные ячейки, получим??1?110?11100. Ответ: (0010110111100).
Пример 2. В коде была допущена одна ошибка: 0010100111100. Найти её.
Решение.
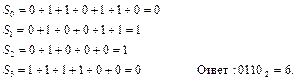
 2015-06-28
2015-06-28 1532
1532








