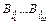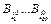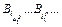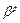2015-06-28
2119
Для каждого элементарного кода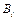 
рассмотрим все нетривиальные представления вида 
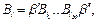(1)
в которых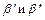 
отличны от элементарных кодов. Обозначим через S множество, содержащее Λ и все 
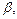встречающиеся в таких разложениях элементарных кодов как в качестве префиксов, так и собственных суффиксов. Сопоставим каждому слову из S точку на плоскости. Вершины 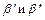соединяем направленным отрезком от 
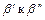для каждого разложения (1) и приписываем этой дуге слово 
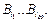Полученный граф обозначим через Г 
.
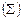ТЕОРЕМА. (Ал. А. Марков). Алфавитное кодирование со схемой å не обладает свойством взаимной однозначности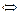 
в графе Г 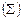существует ориентированный цикл, проходящий через вершину Λ.
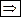Слово 
, допускающее не менее двух расшифровок, называется неприводимым, если каждое слово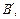 
получающееся из путём выбрасывания непустого подслова, допускает не более одной расшифровки. Пусть алфавитное кодирование не обладает свойством взаимной однозначности. Тогда найдётся неприводимое слово В вида
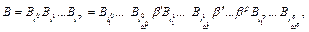
где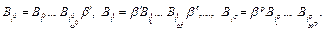 
Отсюда в графе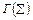 
возникает ориентированный цикл, проходящий через вершину Λ.
|
|
|
 |
|
|
|
|
|
|
|
|
|
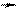
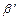
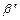
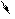В1
|
|
В1
В3
|
|
|
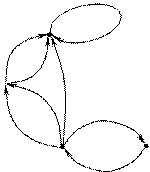
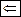Пусть 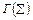содержит ориентированный цикл, проходящий через вершину Λ(рис. 6.1).
Тогда слово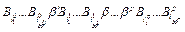 
имеет две расшифровки:
■
|
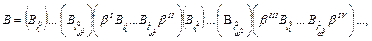
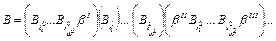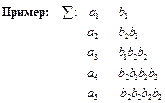
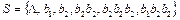
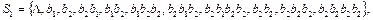
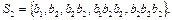
Получим граф, не содержащий ориентированного нетривиального цикла, проходящего через вершину. Следовательно, алфавитное кодирование со схемой å обладает свойством взаимной однозначности.
|
Пусть задано алфавитное кодирование со схемой å: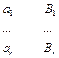 
и пусть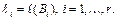 
ТЕОРЕМА. Если алфавитное кодирование со схемой å обладает свойством взаимной однозначности, то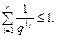 
Доказательство. Все слова длины n в алфавите Â порождены выражением
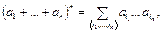(1)
если рассматривать произведение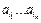 
как запись слова в алфавите Â. Для соответствующих кодов получим
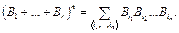(2)
В силу взаимной однозначности алфавитного кодирования, все слагаемые в сумме (2) различны. Всем слагаемым правой части
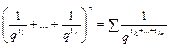(3)
соответствуют слова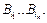 
Введём обозначения: 
, 
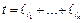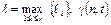– число кодовых слов 
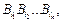имеющих длину t. Тогда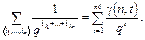 
Из взаимной однозначности кодирования следует:
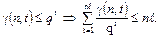
Отсюда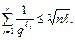 
Это неравенство справедливо для всех n и, следовательно, устремив n к бесконечности, получим утверждение теоремы. ■
Имеет место и обратное утверждение.
|
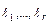удовлетворяют неравенству Макмиллана, то существует алфавитное кодирование со схемой 
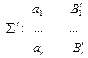, обладающей свойством префикса, где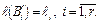 
|
|
|
Доказательство. Пусть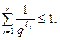 
Можно считать, что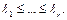 
Пусть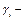 
количество чисел в этой последовательности, равных 
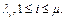Тогда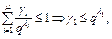 
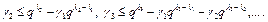
Рассмотрим в алфавите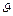 
слова длины 
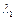. Так как 
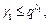то можно выбрать 
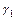слов 
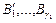длины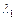 
. Слов длины 
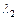, не начинающихся со слов 
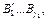имеем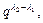 
т.е. можно выбрать такие слова 
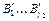и т.д., всего получим 
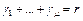слов, т.е. построена искомая схема кодирования, если эти слова взяты в качестве кодовых. ■
Следствие. Если существует взаимнооднозначное алфавитное кодирование, то существует также алфавитное кодирование со схемой, обладающей свойством префикса, и теми же длинами элементарных кодов.
Доказательство. Пусть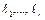 
– длины элементарных кодов взаимнооднозначного кодирования. Эти числа удовлетворяют неравенству Макмиллана, а поэтому существует схема, обладающая свойством префикса, с этими же длинами элементарных кодов. ■
