Пусть имеется источник сообщений, который случайным образом последовательно порождает буквы алфавита Â 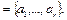 Появления букв статистически независимы и подчинены распределению вероятностей
Появления букв статистически независимы и подчинены распределению вероятностей 
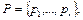 где
где 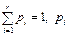 >0. Рассмотрим схему алфавита кодирования å:
>0. Рассмотрим схему алфавита кодирования å: 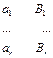 в алфавите Â
в алфавите Â 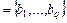 со свойством взаимной однозначности. Пусть
со свойством взаимной однозначности. Пусть 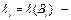 длина слова
длина слова 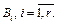 Введём стоимость кода при распределении P как математическое ожидание длины элементарного кода, т.е.
Введём стоимость кода при распределении P как математическое ожидание длины элементарного кода, т.е. 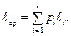 Если
Если 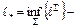 нижняя грань
нижняя грань 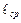 по всем таким схемам å, то
по всем таким схемам å, то 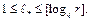 Это следует из того, что всегда можно взять в качестве кодов слова в алфавите
Это следует из того, что всегда можно взять в качестве кодов слова в алфавите 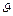 одинаковой длины
одинаковой длины 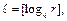 а для такой схемы
а для такой схемы 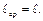
ТЕОРЕМА. Величина 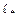 достигается на некоторой схеме å.
достигается на некоторой схеме å.
Доказательство. Для схемы, близкой к 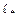 , в силу неравенства
, в силу неравенства 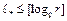 имеем
имеем 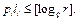 Положив
Положив 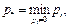 заметим, что
заметим, что 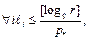 а значит, существует лишь конечное число вариантов значений
а значит, существует лишь конечное число вариантов значений 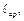 для которых
для которых 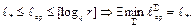 ■
■
Коды стоимости 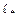 называются оптимальными или кодами с минимальной избыточностью.
называются оптимальными или кодами с минимальной избыточностью.
ТЕОРЕМА. Если 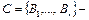 оптимальный двоичный код при распределении
оптимальный двоичный код при распределении 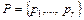 (1)
(1)
и 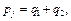 причём
причём 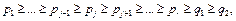 то код
то код 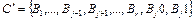 является оптимальным при распределении
является оптимальным при распределении 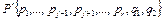 . (2)
. (2)
Доказательство. Если 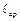 и
и 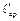 – стоимости кодов при распределениях (1), (2), то
– стоимости кодов при распределениях (1), (2), то 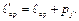 Действительно,
Действительно,
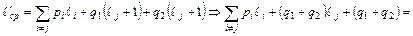
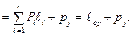
Пусть 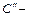 оптимальный код при распределении (2). Тогда в нём длины слов, соответствующих вероятностям q1 и q2, одинаковы, так как код оптимальный. На основе
оптимальный код при распределении (2). Тогда в нём длины слов, соответствующих вероятностям q1 и q2, одинаковы, так как код оптимальный. На основе 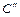 можно построить схему кодирования при распределении (1). Для его стоимости
можно построить схему кодирования при распределении (1). Для его стоимости 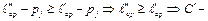 оптимальный код. ■
оптимальный код. ■
На эту теорему опирается алгоритм построения оптимального кода Хафмана.
Пример. Построить оптимальный код по алгоритму Хафмана для распределения вероятностей 0,4; 0,2; 0,2; 0,1; 0,1.
| i | Pi | Bi | |||||||
| 0,4 | 0,4 | 0,4 | 0,6 | ||||||
| 0,2 | 0,2 | 0,4 | 0,4 | ||||||
| 0,2 | 0,2 | 0,2 | 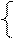 000 000 |            001 001 | |||||
| 0,1 | 0,2 | ||||||||
| 0,1 |
 2015-06-28
2015-06-28 2122
2122








