Детерминированная функция называется ограниченно-детерминированной, если она имеет конечный вес. Класс всех ограниченно-детерминированных функций обозначается 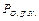 Для ограниченно-детерминированные функции усеченное дерево будет конечным. Если в этом усеченном дереве произвести отождествление вершин с одинаковыми номерами, то получим диаграмму Мура.
Для ограниченно-детерминированные функции усеченное дерево будет конечным. Если в этом усеченном дереве произвести отождествление вершин с одинаковыми номерами, то получим диаграмму Мура.
Пример. Для 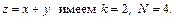 Очевидно, что
Очевидно, что
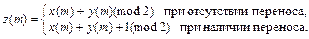
Отсюда дерево имеет вид, изображенный на рис. 10.5.
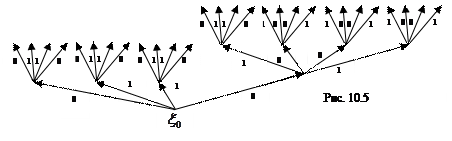
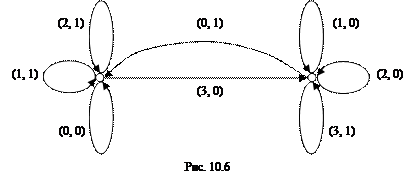
На рис. 10.6 приведена диаграмма Мура для функции 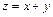 .
.
Нулем отмечена начальная вершина, и для удобства ребрам приписаны пары чисел 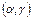 , первые из которых обозначают номер ребра, а вторые – число, соответствующее этому ребру.
, первые из которых обозначают номер ребра, а вторые – число, соответствующее этому ребру.
Диаграмма Мура функции веса 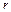 имеет
имеет 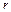 вершин. Одна из вершин выделена в качестве начальной. Из каждой вершины исходит
вершин. Одна из вершин выделена в качестве начальной. Из каждой вершины исходит 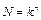 ребер. Ребрам приписаны пары
ребер. Ребрам приписаны пары 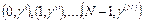 .
.
Диаграммы, удовлетворяющие данным свойствам, также будем называть диаграммами Мура. Диаграммы Мура позволяют строить ограниченно-детерминированные функции любого веса. Формально по заданной диаграмме Мура ограниченно-детерминированные функции восстанавливается однозначно. Однако, если по этой ограниченно-детерминированной функции построить диаграмму Мура, то она может не совпасть с исходной.
ТЕОРЕМА. Число 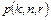 ограниченно-детерминированных функций, зависящих от
ограниченно-детерминированных функций, зависящих от 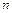 переменных веса
переменных веса 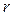 из
из 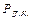 , не превосходит
, не превосходит 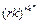 .
.
Доказательство. Возьмем диаграмму Мура для ограниченно-детерминированной функции веса 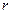 . В ней из каждой вершины исходит
. В ней из каждой вершины исходит 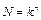 ребер, причем ребро
ребер, причем ребро 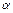 соединено с одной из
соединено с одной из 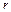 вершин и ему приписана пара (
вершин и ему приписана пара (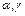 ), где 0
), где 0 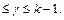 Таким образом, число
Таким образом, число 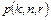 не превосходит числа диаграмм Мура такого вида.
не превосходит числа диаграмм Мура такого вида.
Возьмем теперь 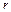 вершин, занумерованных числами 0, 1,…,
вершин, занумерованных числами 0, 1,…, 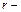 1 (0 – выделенная вершина); из каждой из них исходит по
1 (0 – выделенная вершина); из каждой из них исходит по 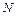 ребер, занумерованных числами 0, 1,…, N – 1. Всего имеем
ребер, занумерованных числами 0, 1,…, N – 1. Всего имеем 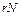 ребер. Каждое ребро может быть соединено с любой из
ребер. Каждое ребро может быть соединено с любой из 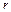 вершин, и ему может быть приписано любое из
вершин, и ему может быть приписано любое из 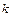 чисел. Поэтому число диаграмм Мура равно числу размещений с повторениями из
чисел. Поэтому число диаграмм Мура равно числу размещений с повторениями из 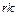 по
по 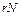 , т.е.
, т.е. 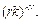 ■
■
 2015-06-28
2015-06-28 1870
1870








