Вес дерева

Для некоторой детерминированных функций 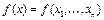возьмем занумерованное дерево. Пусть 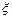– его произвольная вершина m -го яруса. Совокупность всех ветвей, исходящих из 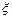, порождает некоторое дерево с корнем 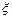, которое называется специальным поддеревом. Так как исходное дерево занумеровано, то поддерево также является занумерованным. Если в поддереве ввести нумерацию, начиная с первого яруса, то ему будет соответствовать детерминированная функция 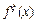. Для нее .

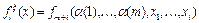Два поддерева с корнями 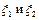исходного дерева называются эквивалентными, если 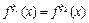. Очевидно, что при естественном наложении двух эквивалентных поддеревьев их нумерации совпадают. В исходном дереве множество всех поддеревьев разбивается на классы эквивалентности. Число классов эквивалентности называется весом дерева и соответственно весом детерминированной функции. Данное определение может быть распространено и на константы. Последовательность 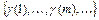изображается вырожденным деревом, состоящим из одной ветви (рис. 10.4).

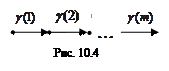В нем можно рассматривать поддеревья и определить эквивалентность поддеревьев. Иначе говоря, вес – это максимальное число попарно неэквивалентных поддеревьев. При этом не исключается случай, когда вес r бесконечен.