ТЕОРЕМА. Класс детерминированных функций замкнут относительно операции суперпозиции. ■
ТЕОРЕМА. Класс ограниченно-детерминированных функций замкнут относительно суперпозиции. 
Доказательство. Пусть 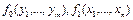 – две ограниченно-детерминированные функции. Рассмотрим функцию
– две ограниченно-детерминированные функции. Рассмотрим функцию 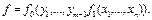 Выпишем канонические уравнения для
Выпишем канонические уравнения для 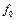 и
и 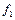 :
:
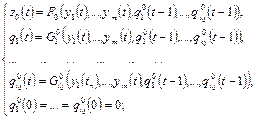
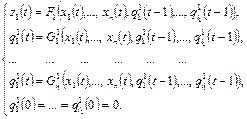
Покажем, что 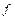 можно задать каноническими уравнениями.
можно задать каноническими уравнениями.
Пусть 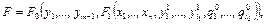
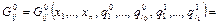
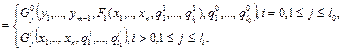
Тогда уравнения
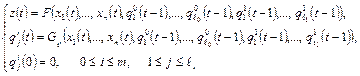
задают ограниченно-детерминированную функцию. Повторив эти рассуждения несколько раз, можно доказать теорему и для любой другой суперпозиции.
Детерминированная функция 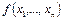 зависит от
зависит от 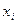 с запаздыванием, если для любых входных последовательностей
с запаздыванием, если для любых входных последовательностей 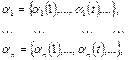
и любого момента времени 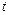 значение
значение 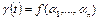 полностью определяется значениями первых
полностью определяется значениями первых 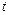 членов последовательностей
членов последовательностей 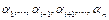 и значениями первых
и значениями первых 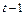 членов последовательности
членов последовательности 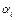 , т.е.
, т.е. 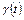 не зависит от
не зависит от 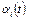 .
.
 Пример. Рассмотрим детерминированную функцию
Пример. Рассмотрим детерминированную функцию 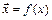 из
из 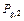 , для которой
, для которой 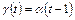 и,
и, 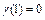 т.е.
т.е. 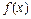 осуществляет сдвиг входной последовательности на один разряд. На рис. 10.7 представлено дерево для
осуществляет сдвиг входной последовательности на один разряд. На рис. 10.7 представлено дерево для 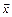 , из которого видно, что
, из которого видно, что 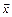 – ограниченно-детерминированная функция веса 2 и имеет канонические уравнения
– ограниченно-детерминированная функция веса 2 и имеет канонические уравнения
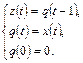
Ограниченно-детерминированная функция 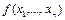 зависит от
зависит от 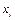 , с запаздыванием
, с запаздыванием 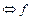 можно задать каноническими уравнениями
можно задать каноническими уравнениями
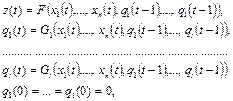
в которых 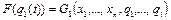 существенно не зависит от
существенно не зависит от 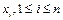 . В приведенном выше примере
. В приведенном выше примере 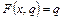 , т.е. не зависит существенно от х.
, т.е. не зависит существенно от х.
 Определим операцию введения обратной связи О. Пусть
Определим операцию введения обратной связи О. Пусть 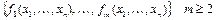 – система детерминированных функций и пусть
– система детерминированных функций и пусть 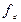 зависит от переменной хj, с запаздыванием. Рассматривая эту систему как преобразователь с n входами и m выходами, соединим выход d с входом j («обратная связь» между выходом d и входом j).
зависит от переменной хj, с запаздыванием. Рассматривая эту систему как преобразователь с n входами и m выходами, соединим выход d с входом j («обратная связь» между выходом d и входом j).
Система канонических уравнений ограниченно-детерминированной функции для 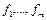 :
:
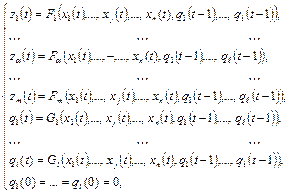
преобразуется к виду
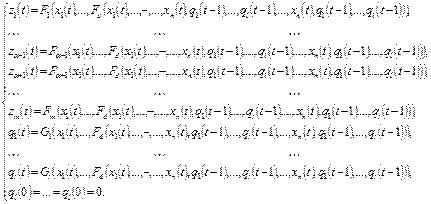 Пример. Рассмотрим систему ограниченно-детерминированной функции, задаваемую каноническими уравнениями:
Пример. Рассмотрим систему ограниченно-детерминированной функции, задаваемую каноническими уравнениями:
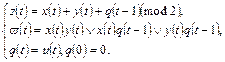
Обе функции 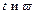 зависят от переменной и, с запаздыванием. Посредством тождества
зависят от переменной и, с запаздыванием. Посредством тождества 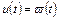 введем обратную связь. Получим канонические уравнения:
введем обратную связь. Получим канонические уравнения:
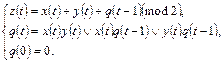
Таким образом, результатом операции О является ограниченно-детерминированная функция, представляющая сложение двух последовательностей.
ТЕОРЕМА. Класс ограниченно-детерминированных функций замкнут относительно операции О. ■
 2015-06-28
2015-06-28 2095
2095








