Задание детерминированных функций деревьями

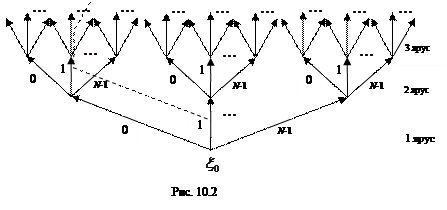
Рассмотрим ориентированное дерево с корнем 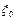, в котором на ярусах расположены по 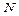ребер, 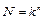(рис. 10.2).

Будем называть ветвью дерева связное подмножество ребер, содержащее в каждом ярусе ровно по одному ребру. Каждой ветви дерева можно сопоставить последовательность 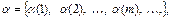где m – номер яруса, 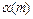– номер ребра, входящего в эту ветвь, если идти по ней, начиная от корня. Например, ветви, помеченной на рис. 10.2 штриховой линией, соответствует последовательность .

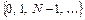Справедливо и обратное утверждение: каждой последовательности соответствует некоторая ветвь дерева.

Пусть y = 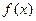– детерминированная функция. При ее помощи припишем каждому ребру дерева число из 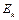. Для этого рассмотрим путь, ведущий от корня к выбранному ребру. Этот путь определен однозначно и может быть охарактеризован некоторым кортежем 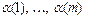номеров ребер пути. Исходному ребру припишем число 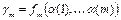. Полученное дерево называется занумерованным деревом.

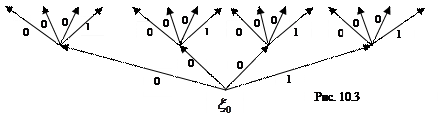
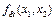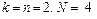Пример. Для функции имеем и 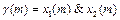. Следовательно, 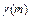зависит от последнего члена кортежа, ведущего к данному ребру, т.е. от номера ребра. Ребру с номером 0 = (0, 0) соответствует значение 0&0 = 0. Ребру с номером 1 = (0, 1) соответствует значение 0&1 = 0, ребру с номером 2 = (1, 0) соответствует 1&0 = 0, с номером 3 – значение 1&1 = 1 (рис. 10.3).

Итак, по детерминированной функции можно построить занумерованное дерево. Обратное утверждение, вообще говоря, неверно. По данному 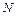, уравнение 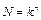может допускать несколько решений относительно параметров k и n. Но по занумерованному дереву с заранее определенными параметрами k и n определится единственная детерминированная функция. Итак, занумерованными деревьями можно пользоваться в качестве аппарата для изучения детерминированных функций.