Полны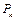е системы

Пусть – множество всех функций k -значной логики, т.е. функций, для которых области определения всех переменных есть множество {0, 1, …, k – 1}, и область значений лежит в этом же множестве.

Примеры функций k -значной логики

1. 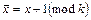– обобщение отрицания в смысле «циклического» сдвига значений;

2. 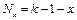– отрицание Лукашевича, другое обобщение отрицания в смысле «зеркального» отображения значений;

3.

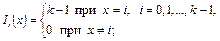
4. 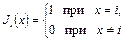– характеристическая функция значения i, 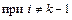представляет собой обобщение отрицания;

5. 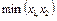– обобщение конъюнкции;

6. 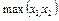– обобщение дизъюнкции;

7. 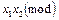– второе обобщение конъюнкции;

8. 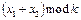– сумма по модулю k;

9. 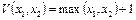– функция Вебба, обобщение функции Шеффера. Функция Вебба образует полную систему в 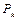относительно операции суперпозиции.

Определим детерминированную функцию 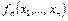для из 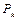следующим образом:

.

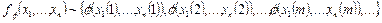Обозначим через 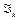множество всех функций, 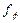где 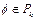. Соответствие 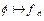порождает отображение 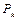на некоторое подмножество 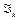ограниченно-детерминированной функции. Оно взаимнооднозначно и сохраняет операцию суперпозиция, т.е. функциональные системы 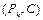и 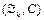изоморфны. Следовательно, в качестве базиса 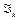можно взять 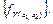Другим примером базиса в 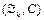является множество .

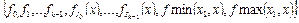ТЕОРЕМА. Система ограниченно-детерминированной функции 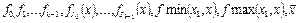полна в 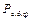относительно операций С и О.

ТЕОРЕМА. Система ограниченно-детерминированной функции 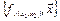полна в 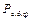относительно С и О.

ТЕОРЕМА. Существует ограниченно-детерминированная функция 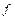– аналог функции Шеффера, такая, что система 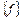полна в 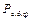относительно С и О.

ТЕОРЕМА. Не существует алгоритма, который бы для каждой конечной системы ограниченно-детерминированной функции выяснял, является ли она полной.

СПИСОК ЛИТЕРАТУРЫ

1. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. – М.: Наука, 1977. - 368 с.

2. Горбатов В.А. Основы дискретной математики. – М.: Высшая школа, 1986. - 311 с.

3. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. – М.: Энергоатомиздат, 1988. - 480 с.

4. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. – М.: Наука, 1984. - 224 с.

5. Москинова Т.И. Дискретная математика. Математика для менеджеров в примерах и упражнениях. – М.: Логос, 2000. - 240с.

6. Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2000. - 304 с.

7. Фудзисава Т., Касами Т. Математика для радиоинженеров. Теория дискретных структур /Пер. с яп. – М.: Радио и связь, 1984. - 240 с.

8. Шоломов Л.А. Основы теории дискретных логических и вычислительных устройств. – М.: Наука, 1980. - 368 с.

9. Яблонский С. В. Введение в дискретную математику. – М.: Наука, 1986. - 384 с.

Дискретная математика

Учебное пособие

Пак Геннадий Константинович,

профессор

ЛР 065166 от 07.05.97

ПЛД №63-67 от 04.06.97

Подписано в печать 23.04.2001

Печать офсетная

Уч.-изд.л. 6,2. Усл. печ. л. 6,0.

Тираж 150 экз.

Институт технологии и бизнеса

692900, Находка, Дальняя, 14

Редакционно-издательский отдел

Института технологии и бизнеса

692900, Находка, Дальняя, 14

Отпечатано в печатном салоне Института технологии и бизнеса

692900, Находка, Дальняя, 14