Матричные игры

Постановка задачи

Пусть у первого игрока имеются ходыА₁,А₂,…А_m а у второго игрока – .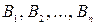

Такая игра называется игрой с нулевой суммой, если ().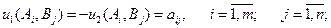

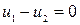Игра называется антагонистической, так как величину, которую выигрывает первый игрок, второй игрок проигрывает.

Игра задается матрицей выигрышей A,

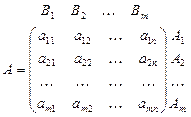(3.1.3)

Отдельный розыгрыш или исход игры осуществляется следующим образом: первый игрок тайным образом выбирает свой ход 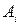(т.е. он выбирает 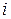-ю строку матрицы 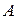), а второй игрок выбирает тайно ход 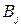( 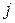- ый столбец матрицы 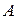). На пересечении 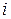-ой строки и 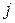-го столбца находится элемент 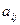. Тогда первый игрок выигрывает это число, а второй проигрывает (должен заплатить ему это число). Понятие “выиграл”и “проиграл” относительные, так как, если 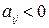, то на самом деле второй игрок получит сумму 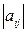, а первый проигрывает .

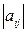Розыгрыши могут повторяться однократно, некоторое количество раз, бесконечно. Ясно, что первый игрок должен выбирать такой свой ход 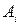, чтобы 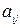было как можно больше (желательно положительным), а второй – 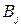таким образом, чтобы 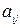было меньше (желательно отрицательным).