Рассмотрим случай, когда 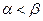 и розыгрыши проводятся многократно. Тогда для первого игрока возникает вопрос: можно ли каким-либо образом чередовать ходы таким образом, чтобы суммарный средний выигрыш был больше
и розыгрыши проводятся многократно. Тогда для первого игрока возникает вопрос: можно ли каким-либо образом чередовать ходы таким образом, чтобы суммарный средний выигрыш был больше 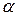 .
.
Аналогично для второго игрока, есть смысл попытаться чередовать свои ходы, чтобы в среднем проиграть меньше 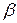 .
.
Определение 9. Вектор 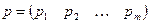 ,
, 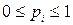 ,
, 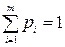 называется смешанной стратегией первого игрока (
называется смешанной стратегией первого игрока (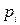 означает вероятность (при бесконечном количестве розыгрышей), либо частоту (при конечном числе розыгрышей), с которой он выбирает свои ходы
означает вероятность (при бесконечном количестве розыгрышей), либо частоту (при конечном числе розыгрышей), с которой он выбирает свои ходы 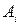 , i=
, i= 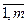 ).
).
Определение 10. Вектор 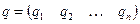 ,
, 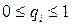 ,
, 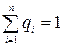 называется смешанной стратегией второго игрока (
называется смешанной стратегией второго игрока (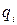 означает вероятность либо частоту, с которой второй игрок выбирает свой ход
означает вероятность либо частоту, с которой второй игрок выбирает свой ход 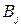 , j=
, j= 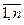 ).
).
Определение 11. Пусть 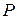 – множество смешанных стратегий первого игрока,
– множество смешанных стратегий первого игрока, 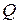 – множество смешанных стратегий второго игрока.
– множество смешанных стратегий второго игрока.
Определение 12: Пусть 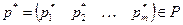 . Тогда, если
. Тогда, если 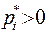 , то ход Ai называется активным ходом, а, если
, то ход Ai называется активным ходом, а, если 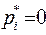 , то он называется пассивным в
, то он называется пассивным в 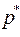 для первого игрока. Аналогично, если
для первого игрока. Аналогично, если 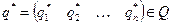 и
и 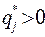 , то ход
, то ход 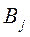 активный, а если
активный, а если 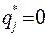 , то этот ход пассивный в
, то этот ход пассивный в 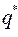 для второго игрока.
для второго игрока.
Замечание: Если в некоторой игре первый игрок все время выбирает ход Ai, то это соответствует смешанной стратегии 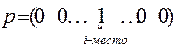 . Аналогично, если второй игрок все время выбирает
. Аналогично, если второй игрок все время выбирает 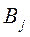 , то тогда
, то тогда 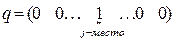 . Тогда Ai и
. Тогда Ai и 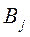 называют чистыми стратегиями игроков.
называют чистыми стратегиями игроков.
Теорема 4 (основная теорема теории игр). В любой матричной игре существует 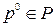 – оптимальная смешанная стратегия первого игрока и
– оптимальная смешанная стратегия первого игрока и 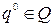 – оптимальная смешанная стратегия второго игрока такие, что:
– оптимальная смешанная стратегия второго игрока такие, что: 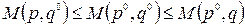 ,
, 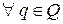 ,
, 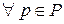 .
.
При этом 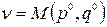 называется ценой игры.
называется ценой игры. 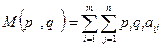 .
.
Можно доказать, что 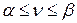 .
.
 2015-06-28
2015-06-28 741
741








