В силу антагонистичности особую роль в матричных играх играет понятие доминирования.
Для первого игрока:
Если при сравнении двух некоторых строк матрицы 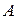 оказывается, что элементы первой меньше либо равны соответствующих элементов второй строки, то это означает, что первая строка доминируется второй строкой (это можно сказать о соответствующих ходах).
оказывается, что элементы первой меньше либо равны соответствующих элементов второй строки, то это означает, что первая строка доминируется второй строкой (это можно сказать о соответствующих ходах).
Ясно, что для этой игры (при любом поведении соперника) доминируемые ходы не следует выбирать и их можно исключить (соответствующую строку вычеркнуть из матрицы 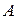 ). А в случае наличия доминирующей строки первый игрок всегда должен выбирать такой ход.
). А в случае наличия доминирующей строки первый игрок всегда должен выбирать такой ход.
Для второго игрока:
Если в матрице 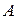 имеется два столбца такие, что элементы первого больше либо равны соответствующих элементов второго столбца, то ему ни при каком поведении соперника нет смысла выбирать первый столбец. И этот столбец называется доминируемым (вместе с ходом) и может быть исключен (вычеркнут) из матрицы
имеется два столбца такие, что элементы первого больше либо равны соответствующих элементов второго столбца, то ему ни при каком поведении соперника нет смысла выбирать первый столбец. И этот столбец называется доминируемым (вместе с ходом) и может быть исключен (вычеркнут) из матрицы 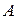 .
.
После исключения доминируемых ходов первого и второго игроков получаем матрицу выигрышей эквивалентную исходной, а в смешанных стратегиях доминируемых ходов первого и второго игроков соответственно 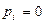 ,
, 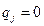 , т.е. доминируемые ходы игроков пассивны.
, т.е. доминируемые ходы игроков пассивны.
Пример 3.1.5. Пусть задана матрица игры. Найти цену игры.
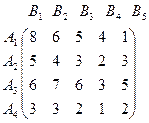
Найдем 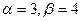 .
.
Ход 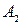 доминируется
доминируется 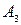 (вычеркиваем
(вычеркиваем 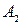 ). Ход
). Ход 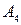 доминируется
доминируется 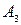 (вычеркиваем
(вычеркиваем 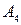 ).
). 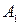 и
и 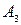 не доминируют друг друга. Ходы
не доминируют друг друга. Ходы 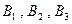 доминируются
доминируются 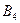 (вычёркиваем
(вычёркиваем 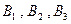 ).
).
В результате упрощения получаем игру эквивалентную исходной:
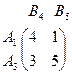
В оптимальной смешанной стратегии первого игрока 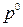 :
: 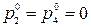 ; второго игрока
; второго игрока 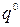 :
: 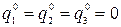 . Соответствующие ходы будут всегда пассивны.
. Соответствующие ходы будут всегда пассивны.
Решение игр 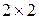 . Геометрическая интерпретация
. Геометрическая интерпретация
Справедлива следующая теорема:
Теорема: пусть первый игрок выбирает 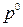 - оптимальную смешанную стратегию, тогда его средний выигрыш все равно будет
- оптимальную смешанную стратегию, тогда его средний выигрыш все равно будет 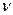 , если другой игрок выбирает любую смешанную стратегию, не выходящую лишь за пределы активных ходов из
, если другой игрок выбирает любую смешанную стратегию, не выходящую лишь за пределы активных ходов из 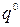 . Аналогичное утверждение справедливо для второго игрока.
. Аналогичное утверждение справедливо для второго игрока.
Замечание. Если ко всем элементам матрицы 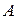 некоторой игры прибавить одну и ту же константу
некоторой игры прибавить одну и ту же константу 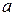 , то это не окажет никакого влияния на оптимальные смешанные стратегии первого и второго игроков, лишь цена новой игры будет равна
, то это не окажет никакого влияния на оптимальные смешанные стратегии первого и второго игроков, лишь цена новой игры будет равна 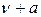 . Поэтому будем считать, что
. Поэтому будем считать, что 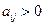 . Тогда и
. Тогда и 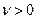 , i=
, i= 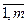 , j=
, j= 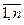 .
.
Такие две игры будут эквивалентными.
Пусть 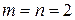 и задана матрица игры.
и задана матрица игры.
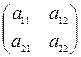 (3.1.6)
(3.1.6)
Пусть в этой игре нет седловой точки, т.е. 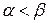 , тогда очевидно, что оба хода и для первого и для второго игроков будут активными.
, тогда очевидно, что оба хода и для первого и для второго игроков будут активными.
Пусть первый игрок придерживается своей стратегии 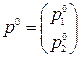 , а второй игрок постоянно выбирает чистый ход
, а второй игрок постоянно выбирает чистый ход 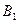 . Тогда по теореме получаем
. Тогда по теореме получаем
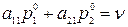 (3.1.7)
(3.1.7)
Если второй игрок все время выбирает 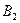 , то
, то
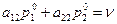 (3.1.8)
(3.1.8)
Добавляя сюда условие
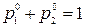 (3.1.9)
(3.1.9)
получаем систему
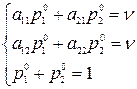
т.е. нахождение оптимальной смешанной стратегии первого игрока и цены задачи сводится к системе (3.1.7), (3.1.8), (3.1.9).
Пусть второй игрок придерживается 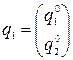 .
.
Тогда, если первый игрок выбирает 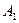 , то его средний проигрыш будет определяться формулой,
, то его средний проигрыш будет определяться формулой,
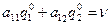 (3.1.10)
(3.1.10)
Если же первый игрок придерживается хода 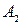 (постоянно), то
(постоянно), то
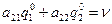 (31.11)
(31.11)
и
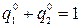 (3.1.12)
(3.1.12)
Получаем систему
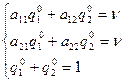 (3.1.3)
(3.1.3)
Таким образом, для решения матричной игры 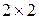 достаточно составить две системы (3.1.7) – (3.1.9), (3.1.10) – (3.1.12) и их решить.
достаточно составить две системы (3.1.7) – (3.1.9), (3.1.10) – (3.1.12) и их решить.
Замечание. При решении этих двух систем, если вначале решить (3.1.7) – (3.1.8) – (3.1.9) и найти цену игры 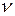 , то
, то 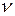 можно подставить в (3.1.10) – (3.1.11) – (3.1.12) и останется система с двумя неизвестными. При таком решении либо формулу (3.1.10) либо формулу (3.1.11) можно исключить.
можно подставить в (3.1.10) – (3.1.11) – (3.1.12) и останется система с двумя неизвестными. При таком решении либо формулу (3.1.10) либо формулу (3.1.11) можно исключить.
Пример 3.1.6. Пусть игра 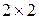 задана матрицей:
задана матрицей:
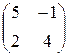
Составим систему уравнений для первого игрока: 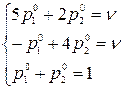
Решением игры будет: 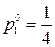 ,
, 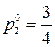 ,
, 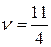 .
.
Составим систему уравнений для второго игрока: 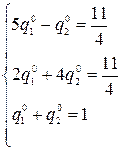
Решением игры будет: 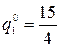 ,
, 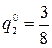 .
.
 2015-06-28
2015-06-28 476
476








