Для первого игрока: Строим систему координат 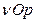 . По оси O
. По оси O 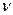 откладываем выигрыш игрока; на отрезке [0,1] по оси Op – его смешанную стратегию.
откладываем выигрыш игрока; на отрезке [0,1] по оси Op – его смешанную стратегию.
Ось ординат соответствуют выбору хода 
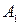 . Прямая p=1 соответствует ходу
. Прямая p=1 соответствует ходу 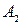 .
.
Если второй игрок выбирает свой ход 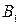 , то выигрыш первого игрока определяется отрезком [5, 2].
, то выигрыш первого игрока определяется отрезком [5, 2].
Если же второй игрок выбирает 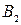 , то выигрыш первого игрока определяется отрезком [–1, 4].
, то выигрыш первого игрока определяется отрезком [–1, 4].
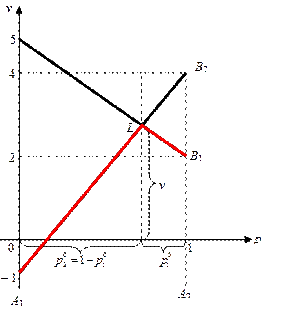
Рис. 3.1.1
Пусть на каждую смешанную стратегию первого игрока второй игрок отвечает наихудшим образом. Тогда выигрыш первого игрока будет определяться нижней ломаной.
Естественно, чтобы в такой ситуации первый игрок выиграл наибольшую величину, он должен подобрать смешанную стратегию, соответствующую высшей точке этой ломаной - 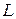 . Абсцисса этой точки определяет оптимальную смешанную стратегию первого игрока, а ордината есть не что иное как цена игры. Это и есть решение системы (3.1.7) – (3.1.8) – (3.1.9).
. Абсцисса этой точки определяет оптимальную смешанную стратегию первого игрока, а ордината есть не что иное как цена игры. Это и есть решение системы (3.1.7) – (3.1.8) – (3.1.9).
Для второго игрока:
Строим систему координат 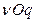 . На O
. На O 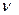 откладываем выигрыш игрока, на [0,1] – смешанную стратегию.
откладываем выигрыш игрока, на [0,1] – смешанную стратегию.
Ось ординат соответствует ходу 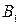 . Прямая q=1 – ходу
. Прямая q=1 – ходу 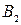 .
.
Если первый игрок выбирает ход 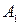 , то выигрыш второго определяется отрезком [5,-1]; если первый игрок выбирает
, то выигрыш второго определяется отрезком [5,-1]; если первый игрок выбирает 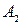 , то у второго игрока выигрыш на [2,4].
, то у второго игрока выигрыш на [2,4].
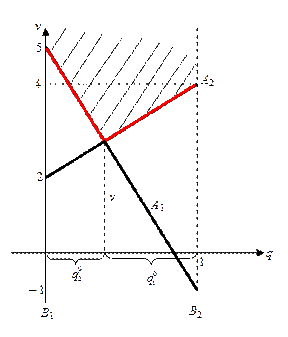
Рис. 3.1.2
Пусть на каждую смешанную стратегию 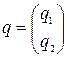 второго игрока первый игрок отвечает наихудшим для него образом.
второго игрока первый игрок отвечает наихудшим для него образом.
Тогда при таком поведении первого игрока проигрыш второго определяется верхней ломаной, а наилучшая смешанная стратегия второго игрока будет соответственно нижней точке 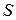 этой ломаной. Абсцисса точки
этой ломаной. Абсцисса точки 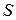 задает оптимальную смешанную стратегию второго игрока, а ордината – цену игры. Это и есть решение системы (3.1.10) – (3.1.11) – (3.1.12).
задает оптимальную смешанную стратегию второго игрока, а ордината – цену игры. Это и есть решение системы (3.1.10) – (3.1.11) – (3.1.12).
Возможны случаи:
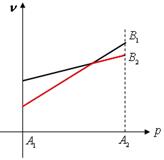  , , 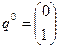 Cедловая точка- Cедловая точка- 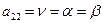 | 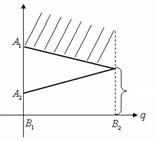 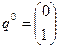 , , 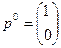 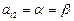 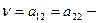 седловые точки седловые точки |
Рис.3.1.3 Рис.3.1.4
Геометрическая интерпретация и решение игр 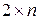 и
и 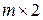
Пусть игра представлена матрицей А1 или А2:
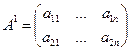 (3.1.14)
(3.1.14)
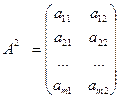 (3.1.15)
(3.1.15)
Используя результаты предыдущего пункта, решение этих игр можно свести к решению двух систем из трех уравнений с тремя неизвестными. Перед тем как составить эти системы нужно решить геометрически эти игры.
Пример 3.1.7. а) случай 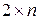 .
.
Пусть игра задана следующей матрицей:
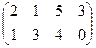
В системе координат 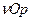 строим отрезки
строим отрезки 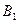 [2,1];
[2,1]; 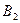 [1,3];
[1,3]; 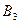 [5,4];
[5,4]; 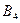 [3,0].
[3,0].
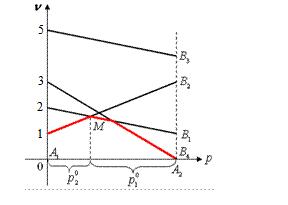
Рис. 3.1.5
Затем строим нижнюю ломаную (это линия наихудшего ответа второго игрока на каждую смешанную стратегию первого), определяем её высшую точку 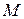 .(см. Рис.3.1.5). По этому графику приближенно можно посчитать
.(см. Рис.3.1.5). По этому графику приближенно можно посчитать 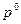 - оптимальную смешанную стратегию первого игрока и цену игры
- оптимальную смешанную стратегию первого игрока и цену игры 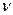 . Для нахождения их точного значения определяем, что в точке
. Для нахождения их точного значения определяем, что в точке 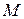 пересекаются
пересекаются 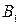 и
и 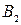 (соответствующие ходы второго игрока будут активными в
(соответствующие ходы второго игрока будут активными в 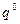 ). Следовательно, исходная игра эквивалентна игре
). Следовательно, исходная игра эквивалентна игре 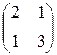 .
.
По этой матрице составляем алгебраические системы (игра 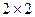 )
)
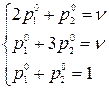
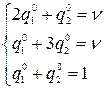
Ответ: 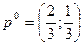 ;
; 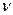 = 1;
= 1; 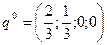 .
.
Общая схема решения игры 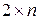
1. вводим систему координат 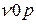 и проводим линию
и проводим линию 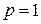
2. для каждого хода 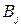 строим соответствующий отрезок, j=
строим соответствующий отрезок, j= 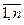
3. строим нижнюю ломаную из кусков 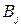
4. находим верхнюю точку этой нижней ломаной и определяем какие ходы второго игрока будут активными в игре (пересекаются в этой точке)
5. строим эквивалентную игру 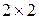 и две алгебраические системы для нахождения оптимальных стратегии (
и две алгебраические системы для нахождения оптимальных стратегии (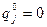 для пассивных ходов).
для пассивных ходов).
Пример 3.1.8. б) случай 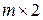 , пусть задана матрица:
, пусть задана матрица:
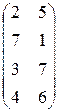
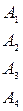
Строим верхнюю ломаную. Находим нижнюю точку 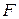 . В точке
. В точке 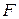 пересекаются
пересекаются 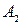 и
и 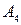 .(см.Рис.3.1.6) Исходная игра эквивалентна игре:
.(см.Рис.3.1.6) Исходная игра эквивалентна игре: 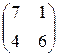 .
.
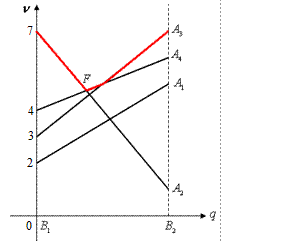
Рис.3.1.6
По этой матрице составим алгебраические системы (игра 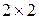 ):
):
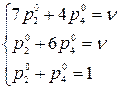
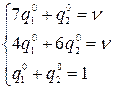 .
.
Ответ: 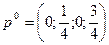 ;
; 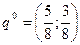 ;
; 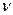 =
= 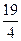
Схема решения игры 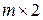
1. строим систему координат 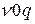 и проводим линию
и проводим линию 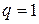
2. для каждого хода 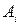 строим соответствующий отрезок, i=
строим соответствующий отрезок, i= 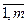
3. находим верхнюю ломаную из этих отрезков
4. определяем нижнюю точку этой ломаной и определяем какие ходы первого игрока будут пересекаться в ней, т.е. являться активными
5. составляем пару алгебраических систем и определяем оптимальные смешанные стратегии игроков и 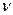 .
.
 2015-06-28
2015-06-28 895
895







