Пусть необходимо исчислить частное корреляционное отношение rAB.C, т.е. найти тесноту корреляционной связи явлений А и В при предварительной фиксации в них той части рассеяния значений, которая вызвана общими причинами с явлением С. Фиксация влияния С осуществляется следующей процедурой:
1. Строим ту часть А, в которой фиксировано остаточное рассеяние А при стабилизации С;
2. Строим ту часть В, в которой фиксировано остаточное рассеяние В при стабилизации С;
3. Коррелируя полученные таким образом элементы остаточного рассеяния, получаем требуемое корреляционное отношение.
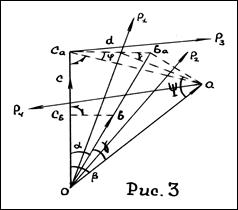 |
При этом необходимо трижды решать задачу сопоставимости. Дабы не загромождать рисунок, воспользуемся уже известным результатом: вектор, фиксирующий рассеяние А при стабилизации В, получим, опуская перпендикуляр 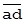 на
на  . На Рис. 3
. На Рис. 3 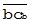 фиксирует рассеяние В при стабилизации С (в масштабе В);
фиксирует рассеяние В при стабилизации С (в масштабе В); 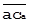 фиксирует остаточное рассеяние А при стабилизации С в масштабе А. Для коррелирования
фиксирует остаточное рассеяние А при стабилизации С в масштабе А. Для коррелирования 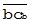 и
и 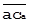 необходимо
необходимо 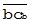 тоже привести к масштабу явления А. Можно убедиться в том, что опять же в предположении линейного закона связи общих частей явлений это осуществимо путём параллельного переноса и
тоже привести к масштабу явления А. Можно убедиться в том, что опять же в предположении линейного закона связи общих частей явлений это осуществимо путём параллельного переноса и 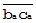 есть
есть 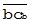 уже в масштабе А. Для коррелирования сопоставленных величин опускаем перпендикуляр
уже в масштабе А. Для коррелирования сопоставленных величин опускаем перпендикуляр 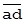 на
на 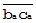 . Отношение ║
. Отношение ║ 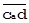 ║ к ║
║ к ║ 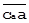 ║ даёт частное корреляционное отношение rAB.C.
║ даёт частное корреляционное отношение rAB.C.
Найдём геометрический аналог полученного построения. Поскольку ∆ cada – прямоугольный с прямым углом при вершине d, то частное корреляционное отношение rAB.C = cos φ. Используя стереометрические приёмы выражения угла φ при основании пирамиды через углы при её вершине, в [7] показано, что cos φ = (cos γ – cos α * cos β) / (sin α * sin β), или, что то же rAB.C = (rAB – rBC * rAC) / (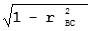 *
* 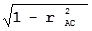 ), что соответствует выражению (3).
), что соответствует выражению (3).
Предложение 3: При линейной форме связи группы случайных величин их частные корреляционные отношения совпадает с частными коэффициентами корреляции.
В Таблице 3 приводится следующая схема построения частного корреляционного отношения:
Таблица 3
Схема исчисления частного корреляционного отношения
| № п/п | Логические операции | Содержание операции для случая линейной регрессии |
| Исчисление единиц масштаба А, В и С | SA = 1 / ║  ║, SB = 1 / ║ ║, SB = 1 / ║  ║, SС = 1 / ║ ║, SС = 1 / ║ 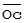 ║ ║
| |
| Сопоставление пар А и С, ВиС | Переход к 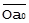 = =  * SA, * SA, 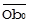 = =  * SB, * SB, 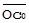 = = 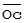 * SС * SС
| |
| Стабилизация С | Аналогично операции стабилизации в схеме 1 | |
| Коррелирование А и С, ВиС | rAС = (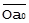 , , 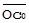 ), rBС = ( ), rBС = (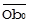 , , 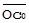 ) )
| |
| Очистка А от С, ВотС | 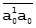 = = 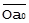 – – 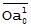 = = 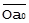 – – 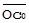 * rAC, * rAC, 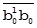 = = 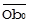 – – 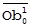 = = 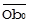 – – 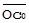 * rBC * rBC
| |
Исчисление единиц масштаба остатков 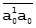 и и 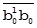
| S(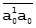 ) = 1 / ) = 1 / 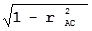 S(
S(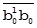 ) = 1 / ) = 1 / 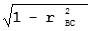
| |
Сопоставление 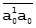 и и 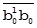
| Переход к 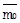 = S( = S(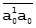 ) * ) * 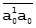
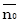 = S( = S(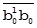 ) * ) * 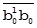
| |
Стабилизация 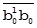
| Аналогично операции стабилизации в схеме 1 | |
Коррелирование остатков 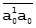 и и 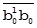
| rAB.C = (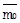 , , 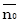 ) )
|
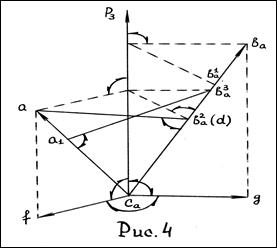 |
Для наглядности частного проецирования часть Рис. 3 выделена в отдельный Рис. 4. 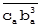 есть
есть 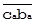 в масштабе
в масштабе 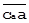 . Опуская из вершины
. Опуская из вершины 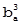 перпендикуляр
перпендикуляр 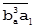 на
на 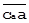 , получим
, получим 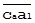 , отражающий тучасть рассеяния значений А (уже предварительно очищенную от влияния С), в которой закреплено рассеяние А, объясняемое линейной зависимостью с В (тоже предварительно очищенным от С). В соответствии с выполненными построениями, в Таблице 4 предлагается следующая логическая схема построения частного показателя взаимосвязи.
, отражающий тучасть рассеяния значений А (уже предварительно очищенную от влияния С), в которой закреплено рассеяние А, объясняемое линейной зависимостью с В (тоже предварительно очищенным от С). В соответствии с выполненными построениями, в Таблице 4 предлагается следующая логическая схема построения частного показателя взаимосвязи.
Таблица 4
Схема исчисления частного показателя взаимосвязи
| № п/п | Логические операции | Содержание операции для случая линейной регрессии |
| Исчисление единиц масштаба А, Ви С | SA = 1 / ║  ║, SB = 1 / ║ ║, SB = 1 / ║  ║, Sс = 1 / ║ ║, Sс = 1 / ║ 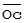 ║ ║
| |
| Представление С в масштабах Аи В | 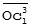 = SС(A) * = SС(A) * 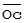 , SС(A) = SС / SА, , SС(A) = SС / SА,
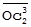 = SС(B) * = SС(B) * 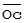 , SС(B) = SС / SB , SС(B) = SС / SB
| |
| Проецирование С на Аи С на В. | ║ 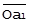 ║ = ║ ║ = ║ 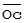 ║ * rAС * SС(A),
║ ║ * rAС * SС(A),
║ 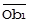 ║ = ║ ║ = ║ 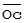 ║ * rBС * SС(B) ║ * rBС * SС(B)
| |
| Очистка А от С и В от С | 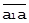 = =  – – 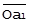 , ,
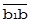 = =  – – 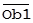
| |
| Исчисление единиц масштаба остатков | S(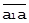 ) = 1 / ║ ) = 1 / ║  ║ * ║ * 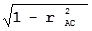 S(
S(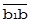 ) = 1 / ║ ) = 1 / ║  ║ * ║ * 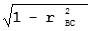
| |
| Представление в масштабе | S = S(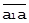 ) / S( ) / S(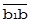 ) )
| |
| Проецирование остатков. Получение частного показателя взаимосвязи | bAB.C = rAB.C * ║  ║ * ║ * 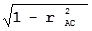 /
║ /
║  ║ * ║ * 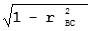
|
Выражение для bAB.C соответствует (3) – (5). Тем самым обосновано:
Предложение 4: При линейной форме связи группы случайных величин их частные показатели взаимосвязи совпадает с частными коэффициентами регрессии.
 2015-06-28
2015-06-28 291
291








