Предлагаемая работа является попыткой индуктивного исследования в области корреляционно – регрессионного анализа. В целом мы пытались следовать фундаментальной схеме правдоподобных рассуждений [1]: Если из А следует В, и В истинно, то А – более правдоподобно. Здесь: А – предлагаемые схемы исчисления показателей; В – соответствующие результаты теории линейной регрессии.
Реализация идей корреляционно – регрессионного анализа тормозится узкими рамками его теории и известной расплывчатостью вероятностных концепций, не позволяющих создать завершенного исчисления вероятностей. Наиболее распространённая в настоящее время (эта рукопись написана в 1976 г.) концепция объективной вероятности исследует массовые явления и не применима для изучения индивидуальных объектов. Реальной действительностью чаще дана случайная последовательность – подходы к её стохастическому рассмотрению необходимо должным образом аксиоматизировать и на этой основе перестроить исчисление вероятностей. Развитие теории вероятностей в этом направлении, основанное на формализуемом в теории алгоритмов понятии сложности случайной последовательности, осуществляется в работах А. Н. Колмогорова, П. Мартин – Лёфа, Соломонова, Шнорра, Я. М. Бардзиня, М. И. Кановича, Н. В. Петри и других исследователей (см. по этому поводу [2 – 4]). Но и к настоящему времени, похоже, не снят вывод работы [3]: «Для того чтобы с полной обоснованностью применять теорию вероятностей к практике, необходимо чётко сформулировать её физическую интерпретацию. Удовлетворительного решения этой задачи до недавних пор получить не удавалось».
Известны общематематические требования корректности Адамара. Эти требования казались настолько естественными для любой математической задачи, что Адамар высказал мысль о нефизичности некорректных постановок. В дальнейшем классические требования корректности Адамара были обобщены А. Н. Тихоновым посредством определения условно корректных постановок. Для задачи, приводимой к решению уравнения
A * u = f, (1)
где А – оператор с непустой областью определения DA, действующий из метрического пространства U в метрическое пространство F: u Î U, f Î F, требования корректности Тихонова формулируются следующим образом:
1. Априори известно, что решение u существует для некоторого класса данных из F и принадлежит заданному множеству M Î DA;
2. Решение u единственно в классе M;
3. Бесконечно малым вариациям правой части (1), не выводящим решение из класса М, соответствуют бесконечно малые вариации решения (требование устойчивости решения).
С прикладных позиций существенно, что к настоящему времени разработаны численные алгоритмы, реализующие требования к условно корректному решению при достаточно общих предпосылках относительно характера исходной информации.
В статистике требование устойчивости конкретизировано в виде принципов инвариантности решения по наблюдениям и параметрам [5]. К сожалению, численных алгоритмов реализации последних, сравнимых по степени общности с алгоритмами реализации детерминированных принципов корректности, в математической статистике пока нет.
Нам представляется возможным подход к построению вероятностных конструкций, имеющих физические аналоги, основанный на последовательной формализации аспекта сопоставимости разнородных величин. При этом исходим из очевидного положения: операция суммирования имеет очевидный физический смысл только для сопоставимых величин. Объекты X0, X1 … Xn называются сопоставимыми (однородными), если совокупность их измерений 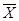 0,
0, 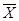 1 …
1 … 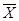 n можно рассматривать как (n+1) независимых выборок наблюдений некоторого гипотетического фактора X*. В противном случае объекты X0, X1 … Xn – разнородны.
n можно рассматривать как (n+1) независимых выборок наблюдений некоторого гипотетического фактора X*. В противном случае объекты X0, X1 … Xn – разнородны.
Приведенное определение однородности недостаточно конкретизировано. В общем случае понятие однородности задаётся введением правила исчисления расстояний 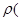 Xi,Xk) для любой пары объектов исследуемого множества X0, X1 … Xn. Для классических условий линейной регрессии, которые будут представлены ниже, такой метрикой однородности является обычное евклидово расстояние [6, стр. 76], т.е.
Xi,Xk) для любой пары объектов исследуемого множества X0, X1 … Xn. Для классических условий линейной регрессии, которые будут представлены ниже, такой метрикой однородности является обычное евклидово расстояние [6, стр. 76], т.е.
rXi,Xk) = ║Xi – Xk║ = 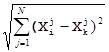
 ,
,
где j - индекс наблюдения в 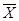 i,
i, 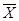 k (j = 1, … N).
k (j = 1, … N).
Главной задачей этой главы является обоснование правил исчисления метрики однородности в неклассическом случае. Для установления возможных аналогий необходимо было уяснить реализацию задачи сопоставимости хотя бы в классическом случае, что позволяет выстраивать дальнейшие построения по индукции. Для реализации этой цели был использован приёмгеометризации доказуемых результатов теории линейной регрессии. Именно это сделало наглядными те свойства объектов, которые обычно скрыты за аналитическими выкладками, и дало возможность догадаться о новых закономерностях. В этом плане мы исходили из работы Н. С. Четверикова, пытаясь выразить те идеи, которые полвека тому (т.е. на момент публикации [7]) звучали отчасти подспудно.
Специфика преследуемых целей требует несколько не традиционной постановки задачи корреляционно – регрессионного анализа. Нетрадиционность здесь состоит в том, что постановка должна быть более содержательной, чем формальной - даже настолько содержательной, чтобы восстановить реально существующее единство детерминированного и стохастического подходов.
Под стохастической величиной понимается многозначимая величина. Способом описания этой многозначимости является определение области возможных значений величины с отнесением к каждому значению вероятности их принятия, т.е. задание закона распределения случайной величины. Итак, стохастичность означает: во-первых, наличие некоторой области рассеяния значений величины; во-вторых, существование некоторой вероятности принятия значения из указанной области. В частности, многозначимость стохастической величины может быть фиксирована заданием «эллипсоида концентрации» – такой области, в которой векторы значений величины одинаково равномерно распределены, имея внутри эллипсоида постоянную плотность вероятности и нулевую плотность вероятности вне его, и для которых совпадают корреляционные матрицы и математические ожидания [8 – 9].
Итак, пусть система из n+1 случайных величин (факторов) X0, X1 … Xn представлена N – мерными векторами наблюдений по каждой величине 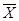 0,
0, 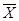 1 …
1 … 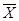 n. В соответствии с принципом множественности причин и следствий А. А. Чупрова, Рюмелина и Янсона, значения каждой величины формируются под влиянием комплекса существенных и несущественных причин. Если какая-то группа причин этого комплекса является общей для двух или более факторов, то это вызывает, в частности, их корреляционную зависимость. Под корреляционной зависимостью понимается такой тип связи величин, когда изменение рассеяния одной или группы величин ведет к изменению условных математических ожиданий и условных дисперсий других величин рассматриваемой системы. Для упорядочения выделения корреляционных связей в системе предложена идея регрессий. Регрессия – это неслучайная функция, связывающая условные математические ожидания (или условные дисперсии) одной величины со значениями других величин рассматриваемой системы. В общем случае идеи корреляционно – регрессионного анализа реализуются комплексом различных видов корреляционных отношений и показателей взаимосвязи. Термин «показатель взаимосвязи» вводится здесь как обобщение понятия «коэффициент регрессии» аналогично тому, как «корреляционное отношение» является обобщением «коэффициента корреляции» на случай неклассических предпосылок. При этом необходимо, чтобы корреляционные отношения отражали относительную силу влияния на рассеяние значений выделенного признака частного комплекса общих причин, связывающих некоторую группу величин, по сравнению с силой всего комплекса причин. От показателей взаимосвязи требуется, чтобы посредством их выражались значения наблюдений некоторой выделенной величины системы (результативного фактора) через наблюдения других величин (затратных факторов), корреляционно связанных с результативным. Таким образом, показатель взаимосвязи должен отображать соотношение масштабных единиц результативного и затратного факторов. Итак, в задаче корреляционно – регрессионного анализа по
n. В соответствии с принципом множественности причин и следствий А. А. Чупрова, Рюмелина и Янсона, значения каждой величины формируются под влиянием комплекса существенных и несущественных причин. Если какая-то группа причин этого комплекса является общей для двух или более факторов, то это вызывает, в частности, их корреляционную зависимость. Под корреляционной зависимостью понимается такой тип связи величин, когда изменение рассеяния одной или группы величин ведет к изменению условных математических ожиданий и условных дисперсий других величин рассматриваемой системы. Для упорядочения выделения корреляционных связей в системе предложена идея регрессий. Регрессия – это неслучайная функция, связывающая условные математические ожидания (или условные дисперсии) одной величины со значениями других величин рассматриваемой системы. В общем случае идеи корреляционно – регрессионного анализа реализуются комплексом различных видов корреляционных отношений и показателей взаимосвязи. Термин «показатель взаимосвязи» вводится здесь как обобщение понятия «коэффициент регрессии» аналогично тому, как «корреляционное отношение» является обобщением «коэффициента корреляции» на случай неклассических предпосылок. При этом необходимо, чтобы корреляционные отношения отражали относительную силу влияния на рассеяние значений выделенного признака частного комплекса общих причин, связывающих некоторую группу величин, по сравнению с силой всего комплекса причин. От показателей взаимосвязи требуется, чтобы посредством их выражались значения наблюдений некоторой выделенной величины системы (результативного фактора) через наблюдения других величин (затратных факторов), корреляционно связанных с результативным. Таким образом, показатель взаимосвязи должен отображать соотношение масштабных единиц результативного и затратного факторов. Итак, в задаче корреляционно – регрессионного анализа по 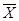 0,
0, 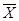 1 …
1 … 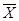 n необходимо:
n необходимо:
1. Обосновать формы зависимости (регрессий) в системе;
2. Построить корректные точечные и интервальные оценки различных видов тесноты и формы связи.
Частным случаем комплекса корреляционных отношений и показателей взаимосвязи является комплекс различных видов коэффициентов корреляций и регрессий. Для условий множественной линейной регрессии Д. Э. Юл показал, что коэффициенты регрессии {bi} модели
E(X0 / X1, X2 … Xn) = b0 + 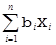 , (2)
, (2)
(где E(X0 / X1, X2 … Xn) – принятоеобозначение функции условного математического ожидания) выражает усреднённое изменение результативного фактора X0, вызванное изменением фактора Xi на единицу его измерения, если при этом влияния прочих затратных факторов остались фиксированными. Усложним систему обозначений в (2): вместо обозначения множественного коэффициента регрессии bi вводится b0i.1,2,...(i-1),(i+1),...n. Здесь: “ 0” - индекс результативного фактора; “ i ” – индекс затратного фактора, непосредственно связанного с результативным; “ 1,2,… (i-1),(i+1),… n ” – индексы затратных факторов, влияние которых фиксировано. Количество фиксированных факторов называется порядком показателя. Аналогично изменяются обозначения частных корреляций r0i.1,2,...(i-1),(i+1),...n; коэффициентов частных дисперсий δ0.1,2,...n; коэффициента совокупной корреляции R0.1,2,...n. В [10] исследована взаимосвязь последующих порядков коэффициентов корреляций и регрессий и доказана справедливость следующих рекурсивных формул:
r0i.1,2,...(i-1),(i+1),...n = 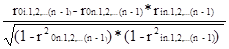 (3)
(3)
δ0.1,2,...n = δ 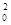 *(1-r
*(1-r 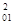 )*(1-r
)*(1-r 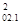 )*(1-r
)*(1-r 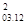 )* … * (1-r
)* … * (1-r 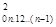 ) (4)
) (4)
b0i.1,2,...(i-1),(i+1),...n = r0i.1,2,...(i-1),(i+1),...n * 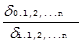 (5)
(5)
δ 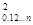 = δ
= δ 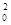 * (1 - R
* (1 - R 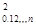 ) (6)
) (6)
b0i.1,2,...(i-1),(i+1),...n = 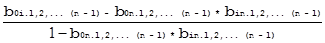 (7)
(7)
Используя известные формулы коэффициентов корреляций и дисперсий нулевого порядка, по (3) – (7) легко построить формальный рекурсивный алгоритм оценивания параметров линейной регрессии.
Для получения по (3) – (7) единственного решения исходная информация 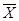 0,
0, 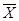 1 …
1 … 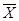 n должна удовлетворять некоторым дополнительным требованиям. Только эффективная оценка – несмещённая оценка с минимальной дисперсией в классе всех несмещённых оценок, для которой достигается нижняя грань неравенства Крамера – Рао [11], удовлетворяет критерию единственности. Формулы (3) – (7) и реализующий их в части коэффициентов регрессии метод наименьших квадратов обеспечивают эффективное оценивание при условии, что выборки Xj = (X
n должна удовлетворять некоторым дополнительным требованиям. Только эффективная оценка – несмещённая оценка с минимальной дисперсией в классе всех несмещённых оценок, для которой достигается нижняя грань неравенства Крамера – Рао [11], удовлетворяет критерию единственности. Формулы (3) – (7) и реализующий их в части коэффициентов регрессии метод наименьших квадратов обеспечивают эффективное оценивание при условии, что выборки Xj = (X 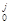 , X
, X 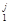 ,… X
,… X 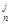 ) являются независимыми случайными выборками из (n+1) – мерной нормально распределённой совокупности [8 – 11]. Там же доказано, что формы регрессий в нормально распределённых совокупностях – линейны. Впрочем, даже эффективное решение не всегда удовлетворяет принципу инвариантности решения по наблюдениям [5].
) являются независимыми случайными выборками из (n+1) – мерной нормально распределённой совокупности [8 – 11]. Там же доказано, что формы регрессий в нормально распределённых совокупностях – линейны. Впрочем, даже эффективное решение не всегда удовлетворяет принципу инвариантности решения по наблюдениям [5].
Понятная ограниченность вводного раздела не позволила в должной полноте рассмотреть возможные содержательные трактовки всех используемых вероятностных понятий (например, процедуры фиксирования влияния прочих затратных факторов, понятия независимости величин и т.п.). С одной стороны, материал рассчитан на достаточно подготовленного в этих вопросах читателя. А с другой - пробелы такого рода, по возможности, будут восполнены в последующих разделах.
 2015-06-28
2015-06-28 329
329








