Геометризация результатов теории линейной регрессии возможна посредством использования аппарата векторной алгебры. Такая возможность появилась с установления изоморфизма между основными операциями векторной алгебры и логическими операциями над случайными величинами (см. по этому поводу, например, [7]). Аппарат векторной алгебры можно применить к решению ряда задач статистики, основанных на тех свойствах векторов, что остаются инвариантными при используемых преобразованиях. Таковыми являются:
1. Длина вектора в евклидовой норме, являющаяся аналогом среднеквадратического отклонения (в предположении предварительного центрирования компонент вектора их среднеарифметическим значением);
2. Величина плоскостного угла между векторами, являющаяся аналогом степени парной корреляционной взаимосвязи;
3. Величина многомерного (объёмного) угла, являющаяся аналогом степени корреляционной зависимости нескольких случайных величин;
4. Проекции приведенных к единому масштабу векторов, являющиеся геометрическими аналогами теоретических значений результативного фактора, объяснимых влияниям соответствующего затратного фактора.
Во всех проводимых в работе построениях первоначально предполагается выполнение предпосылок линейной регрессии.
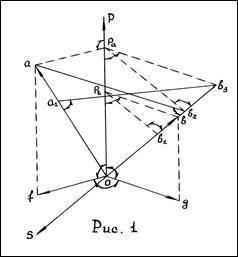 |
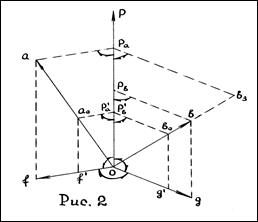
Пусть среди причин, обусловивших рассеяние значений объектов А и В есть группа общих причин и указанные объекты связаны линейной формой зависимости. Рассмотрим логическую структуру показателя, который отображал бы ту долю рассеяния значений А, что вызвана причинами, связанными с В. Исходная информация задана векторами  и
и  . Под вектором понимается элемент N – мерного числового пространства над полем действительных чисел. Предполагается существование единственного вектора направлений общих частей объектов А и В -
. Под вектором понимается элемент N – мерного числового пространства над полем действительных чисел. Предполагается существование единственного вектора направлений общих частей объектов А и В - 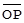 такого, что (см. Рис. 1):
такого, что (см. Рис. 1):
 =
= 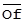 +
+ 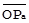 ,
,  =
= 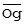 +
+ 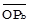 ,
, 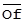 ┴
┴ 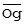 ┴
┴ 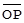 , (8)
, (8)
где 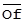 и
и 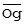 - независимые составляющие А и В;
- независимые составляющие А и В; 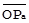 и
и 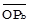 -отражают общую часть рассеяния значений А и В (на рисунке здесь и впредь прямые углы обозначаются дугами с односторонними стрелками). Такое построение основано на том результате, что ортогональность величин в нормально распределённой совокупности является необходимым и достаточным условием их стохастической независимости.
-отражают общую часть рассеяния значений А и В (на рисунке здесь и впредь прямые углы обозначаются дугами с односторонними стрелками). Такое построение основано на том результате, что ортогональность величин в нормально распределённой совокупности является необходимым и достаточным условием их стохастической независимости.
В общем случае явления А и В разнородны по своей природе. Очевидно, что решение задачи сопоставимости связано с масштабированием исходной информации. Так как метрикой однородности в нормально распределённых совокупностях является евклидово расстояние, то за единицу масштаба некоторого фактора в условиях линейной регрессии естественно выбрать величины, обратные к евклидовым нормам векторов исходной информации, т.е. SA = 1 / ║  ║, SB = 1 / ║
║, SB = 1 / ║  ║. Переходом от
║. Переходом от  и
и  к
к 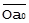 = SA *
= SA *  и
и 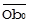 = SB *
= SB *  устраним природную несопоставимость первого рода объектов А и В. Так как корреляционные отношения являются относительными показателями, то в их логических схемах впредь применим только указанный приём снятия несопоставимости.
устраним природную несопоставимость первого рода объектов А и В. Так как корреляционные отношения являются относительными показателями, то в их логических схемах впредь применим только указанный приём снятия несопоставимости.
С другой стороны, несопоставимость связана и с формой взаимосвязи величин. Понятно, что пропорциональная зависимость наблюдённых значений, характерная для линейной регрессии, приведёт к построениям, подобным уже полученным. Поэтому аналитическая задача снятия несопоставимости второго рода состоит в выборе такого масштаба SВ(А), чтобы ║ 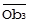 ║ = ║
║ = ║  ║, где
║, где  -вектор явления В в масштабе А. Отсюда SВ(А) = SB / SA. Итак, при линейной форме регрессии геометрическое решение задачи сопоставимости второго рода состоит в проведении Pab3 ║ Pbb (║в данном случаеобозначает символ параллельности) до пересечения с
-вектор явления В в масштабе А. Отсюда SВ(А) = SB / SA. Итак, при линейной форме регрессии геометрическое решение задачи сопоставимости второго рода состоит в проведении Pab3 ║ Pbb (║в данном случаеобозначает символ параллельности) до пересечения с  (см. Рис.2). Так как показатели взаимосвязи являются абсолютными величинами, измеримыми в физических единицах, то в их логических схемах впредь применим только второй приём снятия несопоставимости.
(см. Рис.2). Так как показатели взаимосвязи являются абсолютными величинами, измеримыми в физических единицах, то в их логических схемах впредь применим только второй приём снятия несопоставимости.
 |
Теперь рассмотрим процесс «объяснения» части рассеяния явления А из-за причин, связанных с В. По Рис. 1  =
= 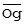 +
+ 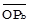 =
= 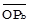 +
+ 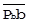 =
= 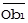 +
+ 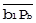 +
+ 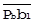 +
+ 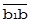 . После стабилизации
. После стабилизации  вектором – стабилизатором
вектором – стабилизатором 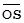 таким, что
таким, что  ║
║ 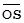 ║ = ║
║ = ║  ║,
║, 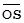 колинеарен
колинеарен  , но противоположен ему по направлению, нейтрализуя внутреннее (т.е. вызванное причинами, не связанными с B) рассеяние значений А, отображённое векторами
, но противоположен ему по направлению, нейтрализуя внутреннее (т.е. вызванное причинами, не связанными с B) рассеяние значений А, отображённое векторами 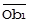 и
и 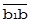 . Остаётся только «внешнее» рассеяние:
. Остаётся только «внешнее» рассеяние: 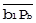 характеризует рассеяние А из-за В в масштабе В;
характеризует рассеяние А из-за В в масштабе В; 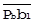 характеризует рассеяние В из-за А в масштабе В. Чтобы внедрить
характеризует рассеяние В из-за А в масштабе В. Чтобы внедрить 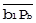 в состав явления А, необходимо привести его к масштабу А. Для случая линейной регрессии так как Δob1Pb ≈ Δob2Pa, то ║
в состав явления А, необходимо привести его к масштабу А. Для случая линейной регрессии так как Δob1Pb ≈ Δob2Pa, то ║ 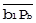 ║ / ║
║ / ║ 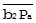 ║ = ║
║ = ║  ║ / ║
║ / ║  ║. Отсюда
║. Отсюда 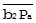 отражает рассеяние значений А из-за В уже в масштабе явления В. Складывая
отражает рассеяние значений А из-за В уже в масштабе явления В. Складывая 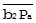 c
c 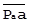 , равным
, равным 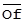 , получим
, получим 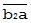 , отражающий явление А после стабилизации В. Векторная разность между
, отражающий явление А после стабилизации В. Векторная разность между  и
и 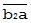 , равная
, равная 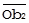 , фиксирует уменьшение рассеяния значений А, произошедшее в результате стабилизации В.
, фиксирует уменьшение рассеяния значений А, произошедшее в результате стабилизации В.
Отношение ║ 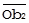 ║ к ║
║ к ║  ║ даёт требуемое корреляционное отношение, измеряющее тесноту связи между А и В. Найдём геометрический аналог построения парного корреляционного отношения, выполненного для условий линейной регрессии. Покажем, что
║ даёт требуемое корреляционное отношение, измеряющее тесноту связи между А и В. Найдём геометрический аналог построения парного корреляционного отношения, выполненного для условий линейной регрессии. Покажем, что 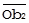 перпендикуляренк
перпендикуляренк  плоскости [ aPab2 ]. Так как
плоскости [ aPab2 ]. Так как  ┴
┴ 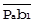 по построению,
по построению,  ┴
┴ 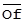 , то
, то  ┴
┴ 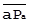 , что и надо было показать. Отсюда Δ ab2O – прямоугольный с прямым углом при вершине b2. Парное корреляционное отношение rAB = ║
, что и надо было показать. Отсюда Δ ab2O – прямоугольный с прямым углом при вершине b2. Парное корреляционное отношение rAB = ║ 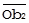 ║ / ║
║ / ║  ║ = cos(ab). Приведенные рассуждения обосновывают
║ = cos(ab). Приведенные рассуждения обосновывают
Предложение 1: Парное корреляционное отношение равно парному коэффициенту корреляции, если закон, связывающий явления, есть линейной регрессией.
Ранее было использовано предположение о том, что существует единственное направление общих частей 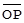 общих частей исследуемых явлений. Легко убедиться в том, что комплекс условий (8) определяет два симметричных направления и выбор одного из них является следствием фиксации наименований результативного и затратного факторов. Если ввести обозначения ‹aOb = α, ‹aOP = β, ‹ bOP = γ, то более компактно положение
общих частей исследуемых явлений. Легко убедиться в том, что комплекс условий (8) определяет два симметричных направления и выбор одного из них является следствием фиксации наименований результативного и затратного факторов. Если ввести обозначения ‹aOb = α, ‹aOP = β, ‹ bOP = γ, то более компактно положение 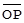 определяется следующими условиями:
определяется следующими условиями:
sin β = sin γ = 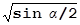 , cos β = cos γ =
, cos β = cos γ = 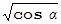 , являющихся следствием (8).
, являющихся следствием (8).
Резюмируя выше изложенное, можно предложить некоторую схему логической структуры парного корреляционного отношения. Здесь и далее в левой части схемы записываются операции для общего случая корреляционных отношений; до выяснения общего способа масштабирования в разделе 5 правая часть схемы является формализацией левой только для условий линейной регрессии.
Таблица 1
Схема исчисления парного корреляционного отношения
| № п/п | Логические операции | Содержание операции для случая линейной регрессии |
| Сопоставление А и В | Переход к 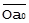 = =  * SA, * SA, 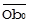 = =  * SB, ║ * SB, ║ 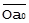 ║ = ║ ║ = ║ 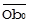 ║ = 1 ║ = 1
| |
| Стабилизация В | Добавление к 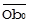 равногои коллинеарного вектора равногои коллинеарного вектора 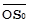 ,но противоположно направленного ,но противоположно направленного
| |
| Коррелирование А и В | rAB = (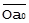 , , 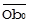 ) = ║ ) = ║ 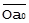 ║ * ║ ║ * ║ 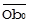 ║ = cos(ab) ║ = cos(ab)
|
В отличие от парного корреляционного отношения, являющегося относительным и неразмерным показателем, показатель парной взаимосвязи является абсолютным и имеющим физическую размерность, выражающим значения явления А через соответствующие значения В. В связи с этим необходимо разграничить употребление терминов «фиксирует» и «отображает». 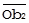 только фиксирует величину уменьшения рассеивания А, произошедшую в результате стабилизации В. Чтобы действительно отобразить ту часть А, которая корреляционно связана с В, необходимо аналогично выше проделанному из b3 опустить перпендикуляр
только фиксирует величину уменьшения рассеивания А, произошедшую в результате стабилизации В. Чтобы действительно отобразить ту часть А, которая корреляционно связана с В, необходимо аналогично выше проделанному из b3 опустить перпендикуляр 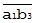 на
на  .
. 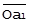 отображает ту часть А, в которойзакреплено рассеяние А, объясняемое причинами, общими с В. Так как ║
отображает ту часть А, в которойзакреплено рассеяние А, объясняемое причинами, общими с В. Так как ║ 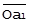 ║ = ║
║ = ║ 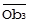 ║ * rAB = ║
║ * rAB = ║  ║ * rAB * ║
║ * rAB * ║  ║ / ║
║ / ║  ║, то показатель взаимосвязи bAB = rAB * ║
║, то показатель взаимосвязи bAB = rAB * ║  ║ / ║
║ / ║  ║, что является частным случаем (5) для нулевого порядка показателя. В обычных терминах корреляционно – регрессионного анализа
║, что является частным случаем (5) для нулевого порядка показателя. В обычных терминах корреляционно – регрессионного анализа 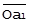 отражает теоретическую (по линейной регрессии) часть результативного признака, или его вариацию, объяснённую затратным фактором В.
отражает теоретическую (по линейной регрессии) часть результативного признака, или его вариацию, объяснённую затратным фактором В.
В Таблице 2 предлагается следующая схема исчисления парного показателя взаимосвязи.
Таблица 2
Схема исчисления парного показателя взаимосвязи
| № п/п | Логические Операции | Содержание операции для случая линейной регрессии |
| Исчисление единиц масштаба А и В | SA = 1 / ║  ║, SB = 1 / ║ ║, SB = 1 / ║  ║ ║
| |
| Представление В в масштабе А | 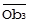 = SB(A) * = SB(A) *  ,
SB(A) = SB / SA = ║ ,
SB(A) = SB / SA = ║  ║ / ║ ║ / ║  ║ ║
| |
| Проецирование В на А. Исчисление парного показателя взаимосвязи | ║ 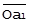 ║ = ║ ║ = ║  ║ * rAB * SВ(A)
bAB = rAB * ║ ║ * rAB * SВ(A)
bAB = rAB * ║  ║ / ║ ║ / ║  ║ ║
|
Введём понятие операции «очистки». Производя векторное вычитание 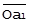 из
из  , получим
, получим 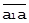 такой, что ║
такой, что ║ 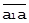 ║2 = ║
║2 = ║  ║2 – b
║2 – b 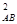 * ║
* ║  ║2 или ║
║2 или ║ 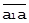 ║ = ║
║ = ║  ║*
║* 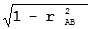 , т.е.
, т.е. 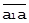 отражает ту часть явления А, в которой закреплено рассеяние, не связанное с В.
отражает ту часть явления А, в которой закреплено рассеяние, не связанное с В. 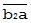 опять же – только фиксирует остаточное рассеяние А.
опять же – только фиксирует остаточное рассеяние А.
Эти построения обосновывают:
Предложение 2: При линейной форме связи случайных величин парный показатель взаимосвязи совпадает с парным коэффициентом регрессии.
 2015-06-28
2015-06-28 411
411








