В общем случае нелинейной взаимосвязи

Итак, решено полностью отказаться от использования неконтролируемых предпосылок относительно совместного закона распределения исследуемой системы стохастических величин. Взамен принята явная ориентация на извлечение возможно полной информации с исходных выборочных данных. Сложность прямого рассмотрения такой задачи понятна хотя бы из направленности исследований, реализующих идеи промежуточных постановок [12 – 15].

В конечном итоге преследуется цель создания конструкций для измерения силы относительной и абсолютной взаимосвязи величин, имеющих очевидные физические аналоги. Предполагается, что такие конструкции обладают свойствами инвариантности. Удалось выяснить, что в случае линейной зависимости соответствующие показатели связи действительно основываются на таких векторных характеристиках, что могут быть инвариантными при некоторых преобразованиях исходной информации. Удалось выделить аспект сопоставимости исходных данных как ключевой момент для попыток обобщения результатов линейной регрессии. Понятно, что в целях сопоставимости можно применять только такие преобразования исходной информации, которые сохраняют скалярное произведение, т.е. относительную силу связи. Последнему требованию удовлетворяют ортогональные операторы. Осталось увязать ортогональные операторы преобразования с исходной информацией.

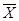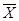Помимо рекурсивных соотношений (3) – (7), задающих полную систему необходимых коэффициентов взаимосвязи, существует сокращённый вариант определения коэффициентов регрессии по методу наименьших квадратов [9]. Пусть по исходным данным ₀, ₁ … 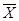_n сформирована матрица X^Т размерности N * (n + 1) следующего вида:

X^Т = , =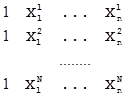

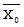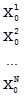
Тогда возможна следующая компактная запись системы нормальных уравнений метода наименьших квадратов:

X * X^T * 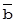= X * ,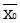

где T – знак операции транспонирования матрицы, b – вектор оценок неизвестных коэффициентов регрессии.

Учитывая также известный результат о произведении ортогональных матриц, естественно предложить следующее определение сопоставимости:

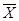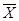Систему выборочных данных ₀, ₁ … 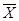_n назовём сопоставимой, если соответствующая матрица X является ортогональной.

Такое предположение удачно согласуется с результатами исследований обусловленности системы линейных алгебраических уравнений. Именно при ортогональной матрице А решение системы A * u = f будет максимально допустимо устойчиво к действию возможных погрешностей в задании исходной информации, а число обусловленности ортогональной матрицы равны 1.

Таким образом, пришли к следующей задаче, которую можно назвать задачей ортогонализации: от некоторой произвольной матрицы X = {x_ij}, i=1,…n, j=1,…N перейти к ортогональной матрице A = {a_ij} той же размерности. Характеристическое свойство ортогональной матрицы A * A^T = A^T * A = E, где E – единичная матрица. Пусть общий вид необходимого преобразования a_ij = u_i * x_ij * v_j. В таком случае условие ортогональности записывается следующим образом:

u_k * u_l * x_kj * (v_j)² = 0, k,l є I, k ≠ l (12)

u_k * u_l * x_kj * (v_j)² = 1, k,l є I, k = l

Итак, исходя из X = {x_ij}, необходимо найти такую систему коэффициентов {u_i, v_j}, которая удовлетворяла бы условиям (12). Такое осуществимо, например, следующим образом:

min max ((u_k)² * (x_kj)² * (v_j)² – 1) (13)

^{{uk, vj} kєJ}

при (N – 1) * n следующих ограничениях:

u_k * u_l * x_kj * (v_j)² = 0 для всех k,l є I, k ≠ l (14)

Возможно упрощение задачи (13)-(14) посредством ввода новых обозначений: b_{k j} = (x_kj)², x_k = (u_k)², y_j = (v_j)². Вопрос возможности точного решения задачи ортогонализации остаётся открытым. Эвристические численные алгоритмы решения подобной задачи рассматриваются в работе [16]. Дело в том, что Дж. Х. Уилкинсон в [17] ввёл понятие уравновешенной квадратной матрицы как такой, у которой евклидовы нормы строк и столбцов совпадают и равны 1. В [16] доказана сходимость при достаточно слабых условиях итерационной процедуры последовательного нормирования строк и столбцов исходной матрицы. Зададимся вопросом: почему математик Уилкинсон ввёл интуитивное понятие уравновешенной матрицы? Подлинные мотивы своего предложения автор не стал раскрывать, но некоторые предположения по этому поводу можно выдвинуть. Понятно, что независимость и производная от неё ортогональность возможны лишь как предельные абстракции, достижимые разве что на высшем уровне организации информации – уровне Абсолюта. Математики отнюдь не чужды философии, Уилкинсон, безусловно, знал о том, что практически все мировоззрения исходят из признания взаимной обусловленности всего сущего во Вселенной. Помимо подлинной свободы (независимости), доступной разве что Творцу Вселенной, должна быть некоторая мера приближения к этому идеалу. Матрица в равновесном состоянии в смысле Уилкинсона, видимо, может выступать носителем этой меры. Соответственно число обусловленности равновесной матрицы может рассматриваться в качестве меры степени свободы соответствующего объекта или субъекта.

Таким образом, метрикой сопоставимости для каждого элемента x_ij матрицы X предлагается выбирать множитель u_i * v_j, полученный при переходе к уравновешенной матрице.

В целом разделяю предположение Стаффорда Бира относительно того, является ли вероятностная система в действительности детерминированной, но не понятой до конца. В продвижении к максимально возможному устойчивому равновесию и заключается эволюция любой системы.

Сигнальный взгляд и волновая природа всего сущего во Вселенной позволяют по-новому взглянуть на содержательный аспект базисной задачи. Любой волновой носитель нижнего уровня по своей сути представляет линейный функционал – волновую спираль, которая в динамике образует объёмный конус, а в плоскостной проекции – некоторую синусоиду. Чтобы передать большее количество информации, необходимо увеличить частотную характеристику сигнала за счёт уменьшения длины его волны. Если представить итерационную процедуру последовательного кратного дробления полупериода синусоиды, то становится понятно, что на некотором этапе волновой параметр начнёт стремиться к нулю, преображаясь в вектор. Линейность означает зависимость следующих состояний этого процесса от предыдущих, порождение массы неустойчивых производных с накоплением структурных деформаций; нелинейность (многомерная объёмность) – это зависимость всех производных состояний от базовой основы. «Фишка» BIP – теории состоит в том, что последовательная линейная схема наследования, ведущая к деформациям и спирализации, заменяется параллельной (нелинейной) схемой наследования от базисной основы, обеспечивая устойчивое выполнение качественной фрактализации.

С остальными аспектами соответствия исходной задачи постулатам BIP – теории дело обстоит гораздо проще: рекурсия корреляционных отношений и показателей взаимосвязи может рассматриваться как частный случай многомерного фрактального клонирования. Как известно из BIP – теории, идеальным объектом фрактализации (в смысле сочетания предельной простоты и возможностей сложной организации) является объёмная сфера. Поэтому любые логические построения (вроде геометрических схем исчисления показателя) должны быть приведены в соответствие со структурой объёмной сферы. Приёмы совместного масштабирования, используемые при уравновешивании матрицы данных, и есть итерационной процедурой для необходимого преобразования в сферу.

Такова общая схема необходимых обоснований. Понимаю, что для доказательства в академическом смысле надо бы, как минимум, привлечь тензорное исчисление и ассоциативную алгебру Клиффорда, но «не силён» в этом аппарате, а посему допускаю ограничиться сугубо индуктивными разъяснениями и прагматическим результатом.

Итак, корректное решение задачи сопоставимости посредством уравновешивания матрицы измерений соционических свойств позволит определить число обусловленности респондента. Можно трактовать число обусловленности матрицы измерений как меру гармоничности личностного сознания или, что то же самое, - как достижимую индивидуумом меру конвертации (в смысле BIP-теории) личного сознания. По мере накопления эмпирического материала, можно будет определить диапазоны значений числа обусловленности, которые соотвтствуют различным уровням конвертации сознания.

Осталось представить конкретный численный алгоритм определения числа обусловленности психоматрицы. Решение системы уравнений Ax=μx относительно μ сводится к решению так называемого характеристического уравнения, которое является алгебраической записью условия

Det(A – E * μ) = 0

Можно свести психоматрицу к частным случаям размерности 3 * 3. В этом предположении, расписав выражение для определителя Det(A–E*μ), и произведя замену μ на привычное обозначение неизвестной величины x, получим каноническую запись кубического уравнения:

x³ + a * x² + b * x + c = 0,

где:

a = -(a₁₁ + a₂₂ + a₃₃);

b = a₁₁ * a₃₃ + a₂₂ * a₃₃ + a₁₁ * a₂₂ - a₁₂ * a₂₁ – a₂₃ * a₃₂ - a₁₃ * a₃₁;

c = -Det (A).

Далее представлен алгоритм для решения этого кубического уравнения методом Виета-Кардано. Для нахождения его корней, в случае действительных коэффициентов, сначала вычисляются:

Q = (a² – 3 * b) / 9,

R = (2 * a³ – 9 * a * b + 27 * c) / 54.

Если R² < Q³, то уравнение имеет три действительных корня, которые вычисляются по формулам Виета:

t = acos(R / sqrt(Q³)) / 3,
x₁ = -2 * sqrt(Q)cos(t) – a / 3,
x₂ = -2 * sqrt(Q) cos(t + (2 * pi / 3)) – a / 3,
x₃ = -2 * sqrt(Q) cos(t - (2 * pi / 3)) –a / 3.

В случае, когда R² >= Q³, действительных корней будет или всего один (общий случай), или два (вырожденный случай). Кроме действительного корня, имеют место два комплексно-сопряженных. Для их нахождения используются формула Кардано:

A = -sign(R)[|R| + sqrt(R² - Q³)]^1/3,
B = Q / A при A ¹ 0 или B = 0 при A = 0.

Действительный корень определяется выражением:

x₁ = (A + B) – a / 3.

Комплексно-сопряженные корни определяются формулами:

x_2,3 = -(A + B) / 2 – a / 3 + i * sqrt(3) * (A - B) / 2

В случае, когда A = B, комплексно-сопряженные корни вырождаются в действительный:

x₂ = -A – a / 3.

Текст исходного модуля PHP -программы для определения собственных чисел уравновешенной психоматрицы, социотипа, витальной и ментальной формул личности, а также оценки её гармоничности (числа обусловленности) представлен в Приложении 3.

Цитированная литература

1. Д. Пойа Математика и правдоподобные рассуждения. М.: «Наука», 1975, ИЛ, 1957.

2. Колмогоров А. Н. К логическим основам теории информации и теории вероятности. «Проблемы передачи информации», 1969, №3.

3. Звонкин А. К., Левин Л. А. Сложность конечных объектов и обоснование понятий информации и случайности с помощью теории алгоритмов. «Успехи математических наук», 1970, т. 25, № 6.

4. Колмогоров А. Н. Сложность задания и сложность построения математических объектов. «Успехи математических наук», 1972, т. 27, № 2.

5. Климов Г. П. Инвариантные задачи в статистике. М.: Издательство МГУ, 1973.

6. Айвазян С. А., Бежаева З. И., Староверов О. В. Классификация многомерных наблюдений. М.: «Статистика», 1974.

7. Четвериков Н. С. Логическая структура методов и показателей теории корреляции, изложенная в векторном отображении. В сборнике «Стохастические и статистические исследования». М.: «Госстатиздат», 1963.

8. Геральд Крамер Математические методы статистики. М.: ИЛ, 1948.

9. Линник Ю. В. Метод наименьших квадратов и основы математико – статистической теории обработки наблюдений. М.: 1962.

10. Юл Д. Э., Кендэл М. Д. Теория статистики. М.: «Госстатиздат», 1960.

11. Климов Г. П. Прикладная математическая статистика, ч. 1. Издательство ВЦ МГУ, 1969.

12. Фаддеев Д. К., Фаддеева В. Н. К вопросу об устойчивости вычислительных алгоритмов. В сборнике «Вычислительные методы линейной алгебры». Новосибирск, издательство СО АН СССР, 1969.

13. Фаддеев Д. К., Фаддеева В. Н. О естественных нормах для оценивания решения конечной вычислительной задачи, ЖВМ МФ, 1969, т. 9, № 1.

14. Фаддеев Д. К., Фаддеева В. Н. Естественные нормы в алгебраических процессах. В сборнике «Вопросы точности и эффективности вычислительных алгоритмов». К.: 1969.

15. Фаддеев Д. К., Фаддеева В. Н. Сопутствующая матрица и оценивание решения конечной вычислительной задачи. В сборнике «Вычислительные методы линейной алгебры». Новосибирск, издательство СО АН СССР, 1973.

16. Шакин В. В. Уравновешивание матрицы данных. В сборнике «Математика и социология». Новосибирск, 1973.

17. Дж. Х. Уилкинсон Алгебраическая проблема собственных значений. М., «Наука», 1970.

ПРИЛОЖЕНИЕ 1