Список літератури. 1. Новиков Ф.А. Дискретная математика для программистов

1 2 3 4 5 6 7

Основна

1. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.23, 24.

2. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. - С.28-34.

3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.89-91.

Додаткова

4. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. – К.:Наук. думка, 1989. - С.22-35.

Для практичних занять

5. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.6-7.

Лекція 3. Упорядковані множини. Графіки

Вступ

Лекція має за мету висвітлити початкові поняття з теорії упорядкованих множин і графіків. Розглянути визначення упорядкованих множин і графіків, операції декартового (прямого) добутку, декартового ступеня, проекції, інверсії, композиції. Звернено повагу до властивостей функціональності та інверсії графіків, а також на властивості розглянутих операцій.

Лекція містить два підрозділи:

3.1. Упорядковані множини

3.2. Графіки

3.1. Упорядковані множини

Усяку множину можна упорядкувати, якщо кожному елементу ії поставити у відповідність деяке натуральне число від 1 до n, де
n - потужність множини. Таке число буде номером елемента.

Визначення. Упорядкованою множиною чи кортежем називається послідовність елементів множини, в якій кожен елемент займає визначене місце, елементи кортежу називаються його компонентами, число компонентів кортежу - n - його довжина

Приклад.А=<1, 2, 3>; B=<2, 1, 2>; C=(a, d, d)

Загальне позначення кортежу − пари кутових <...>, чи круглих (...) дужок, усередині яких задаються в упорядкованому вигляді компоненти кортежу. Конкретні кортежі, як і множини, позначаються великими латинськими літерами А₀, В₄, С_j,..., компоненти кортежів позначаються рядковими латинськими літерами a, b₄, c_j,....

Кортежі вважаються рівними, якщо в них збігаються компоненти і порядок їхнього проходження − А=В, інакше кортежі не рівні − А¹В.

Компонентами кортежу можуть бути елементи множин, множини, інші кортежі. Ще одна назва кортежів - вектори чи n-ки (двійки, трійки,...).

Визначення. Прямим чи декартовим добутком множин А і В називається множина АхВ, що складається зі всіх упорядкованих пар, перший компонент яких належить множині А, а другий компонент належить множині В.

А×В={<a, b>ÎA×В|аÎА і bÎB}

Приклад. А={а, b}; B={1, 2}; A×В={<а, 1>, <а,2>, <b, 1>,<b,2>}.

Очевидно, що якщо ½A½=n, а ½B½=m, то ½AхВ½=n×m.

Визначення. Прямим декартовим добутком множин А₁, А₂,..., А_n називається множина А₁×А₂×...×А_n, із усіх n-к, перший компонент яких належить множині А₁, другий компонент належить множині А₂,..., n-а компонента належить множині А_n:

×А_і=А₁×А₂×... ×А_n={<а₁, а₂,..., а_n>ÎA₁×А₂×...×А_n| a₁ÎA₁, a₂ÎA₂,..., a_nÎA_n}

Визначення. Прямий декартовий добуток множин А₁×А₂×... ×А_n при рівних множинах А₁=А₂=... =А_n=A називається прямим n-м декартовим ступенем множини А і позначається Аⁿ:

Аⁿ=A×А×... ×А = {<a₁, a₂,..., a_n>ÎAⁿ|a₁, a₂,..., a_nÎA}

При n=0 і n=1 по визначенню вважається А⁰={Æ} і А¹=А. Важливою підмножиною декартова добутку А×А є множина D_А={<а, а>|аÎА}, називана діагоналлю, що позначається також як E_A.

До кортежів чи множини кортежів однакової довжини застосовується унарна операція проекції.

Визначення. Проекцією кортежу А на і-ю вісь називається і-я компонента кортежу А, що позначається як пр_іА.

Проектування звичайне ведеться на сукупність упорядкованих по зростанню осей.

Приклад. А=<1, 2, 3, 3, 4>; пр₂А=2; пр₄А=3; пр_1,4А=<1, 3>.

Визначення. Проекцією множини М кортежів довжини n називається множина проекцій усіх кортежей з М

Приклад. М={<1, 2, 2, 3>, <а, b, c, d>, <a, 2, 4, c>}, пр₁М={1, а}; пр₁₃М={<1, 2>, <а, з>, <а, 4>}

Прямі декартові добуток і ступінь мають такими властивостями:

1. А×В¹В×А

2. А×(В×С)¹(А×В) ×С¹А×В×С

3. (АÈВ)×С=(А×С)È(В×С)

4. (АÇВ)×С=(А×С)Ç(В×С)

5. (А\В)×С=(А×С)\(В×С)

6. А×А×... ×А=Аⁿ.

7. А^l×А^м¹А^l⁺^m.

8. А^l×А^м¹А^м×Аа^l.

9. А×Æ=Æ×А=Æ.

3.2. Графіки

Визначення. Множина Р називається графіком, якщо кожен його елемент є двійкою елементів деякої множини М.

Р={рÎR|р=< а, b> і а, bÎМ}

Приклад. Р={<а, b>, <1, c>, <2, 3>}

Якщо М - довільна множина, то М² - графік, будь-яка підмножина множини М² також є графіком.

Визначення. Множина проекцій графіка Р на першу вісь називається областю визначення графіка Р, множина проекцій графіка Р на другу вісь називається областю значень графіка.

Якщо відкласти по осі Х область визначення, а по осі Y область значень, то сам графік розміститься деякім чином на площині (рис. 3.1.).

Якщо графік Р=Æ, то очевидно ін₁Р=Æ і ін₂Р=Æ.

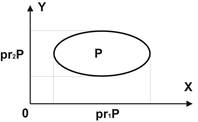
Рис. 3.1. Графік і його проекції на площині

Якщо графік по визначенню є множиною, то над графіками можуть виконуватися операції, що звичайна для множин, тобто È, Ç, \, ù, -.

Визначення. Двійка < с, d> називається інверсією двійки <a, b>, якщо компоненти с дорівнює b, та d дорівнює a.

Інверсія пари р=<а, b> позначається як р^-1.

Подвійна інверсія двійки (р^-1)^-1 дорівнює самій двійці (р^-1)^-1=р.

Визначення. Інверсією графіка Р, що позначається як Р^-1, називається множина інверсій усіх пар з Р

Р^-1={qÎР^-1|q=p^-1 і рÎR}

Приклад. Р={<1, 2 >, < а, b>}, P^-1={<2, 1>, <b, a>}

При інверсії графіка Р пр₁R^-1=пр₂Р і пр₂R^-1=пр₁Р.

Визначення. Графік Р називається симетричним, якщо він поряд з кожною парою містить її інверсію

рÎR Þ р^-1ÎР

Приклад. р={<a, b>, <b, a>, <c, c>}

Для будь-якої множини М множина М² - симетричний графік, для будь-якого графіка Р РÈR^-1 і RÇR^-1 - симетричні графіки.

Визначення. Графік R=P°Q називається композицією графіків Р і Q, якщо двійка <х, у> належить R тоді і тільки тоді, коли існує такий елемент z, що двійка <х, z> належить Р и двійка <z, у> належить Q:

R=P°Q={<х, у>ÎR| існує z такий, що <х, z>ÎR і <z, у>Q}

Приклад. Р={<а, a>, <a, c>, <a, b>, <b, b>, <c, b>}

Q={<a, b>, <a, c>, <c, з>}

R=P_° Q={<a, b>, <a, c>}

Композиція графіків Р и Q порожня тоді, коли пр₂P₁Çпр₁P₂ = Æ.

Визначення. Декартовим добутком Р₁ і Р₂ називається графік

Р₁´Р₂={<<a₁, a₂>, <b₁, b₂>>|<а_і, b_і>ÎR_і, і=1,2}

Визначення. Графік Р називається функціональним, якщо в ньому немає пар з однаковими першими і різними другими компонентами; графік Р називається ін’єктивним, якщо в ньому немає пара з однаковими другими і різними першими компонентами.

Приклад. R₁={<a, b>, <a, з>} нефункціональний

R₂={<a, c>, <b, c>} неін’єктивний

Графік М² на довільній множині М не є функціональним і ін’єктивним, композиція функціональних графіків функціональна, композиція ін’єктивних графіків ін’єктивна, інверсія переводить функціональний графік у ін’єктивний, а ін’єктивний - у функціональний.

Операції над графіками мають спеціальні властивості:

1. Р₁°R₂¹R₂°R₁ не комутативність

2. R₁°(R₂°R₃)=(R₁°R₂)°R₃ асоціативність

3. R°Æ=Æ°R=Æ властивості границь

4. (Р₁°R₂)^-1=R₂^-1°R₁^-1

Контрольні запитання

1. Що таке упорядкована множина та як вона позначається?

2. Яка різниця між декартовим добутком і ступенем?

3. Які проекції можуть бути?

4. Які властивості мають операції над упорядкованими множинами?

5. Що є графіком?

6. Які операції можливі над графіками?