Дистрибутивність

Вступ

Підвищенню рівня математичної підготовки студентів вузів, що особливо спеціалізуються в галузі комп'ютерних систем і мереж, традиційно приділяється велика увага. Особливе значення в цьому плані має вивчення сучасних розділів математики, таких як теорія множин, булева алгебра, теорії графів і автоматів, що є математичною основою для цілого ряду спеціальних дисциплін кібернетичного циклу. Ці розділи заведено відносити до дискретної математики, яка є базою кібернетики.

Запропонований конспект лекцій з дисципліни «Основі дискретної математики» підготовлений відповідно до програми дисципліни, що вивчається студентами інституту комп'ютерних систем ОНПУ. Необхідність видання конспекту обумовлена тим, що склад розділів навчальних посібників, присвячених дискретній математиці і призначених для студентів технічних вузів, не відповідає специфіці викладання в ОНПУ. Даний конспект має за мету дати студенту матеріал для самостійної роботи і більш глибокого засвоєння специфічних математичних знань, а також полегшити викладачам підготовку до проведення занять.

До конспекту включені розділи теорії множин і алгебраїчних систем, комбінаторики, графів, скінченних автоматів і булевої алгебри. Третій і четвертій розділи представлені у вступній формі в зв'язку зі спеціальним, більш вузьким і прикладним їх вивченням у наступних дисциплінах. Конспект викладений з послідовним ускладненням матеріалу, ілюстрований необхідними прикладами та оформлений у вигляді тридцяти шести лекцій, що містять кілька параграфів, супроводжуються вступом, змістом, контрольними запитаннями і літературою. Кожен параграф містить необхідні теоретичні відомості, що являють основні поняття, визначення, операції і властивості. Перелік літератури, що наводиться, не претендуючи на вичерпну повноту, містить навчальні посібники і книги, Якіми може скористатися студент.

У літературі в галузі термінології і позначень є різночитання. У конспекті використовується термінологія і позначення, що прийняті у першоджерелах [1-6] - розділ 1; [2, 3] - розділ 2, [1, 2, 3, 6, 10] – розділ 3, [1, 2, 5, 6, 7, 12] – розділ 4, [1, 2, 4, 6-9] – розділ 5.

Для самостійного вивчення теорії рекомендуються першоджерела: до розділу 1 - [1-3, 5] - основні, [4-6, 12]- додаткові; до розділу 2 - [3] - основні, [1] - додаткові; до розділу 3 - [1, 2, 10]- основні, [11] – додаткові; до розділу 4 - [2, 7, 12]- основні, [11] – додаткові.; до розділу 5 - [1, 9] - основні, [8, 14] – додаткові. Більш докладний матеріал для практики (і для самостійної роботи взагалі) можна знайти в першоджерелах [20-23].

розділ 1. ТЕОРІЯ МНОЖИН І АЛГЕБРАЇЧНИХ СИСТЕМ

Лекція 1. Основні поняття теорії множин

Вступ

Лекція має за мету навести початкові поняття з теорії множин. Розглянуто основні визначення множин та п’яти операцій, існуючі базові вісімнадцять тотожностей і засоби їх доведення. Звернено повагу до узагальнення властивостей множин та операцій і принципу подвійності.

Лекція містить чотири підрозділи:

1.1. Основні поняття і завдання множин

1.2. Операції над множинами. Формули. Тотожності

1.3. Доведення тотожностей. Булева алгебра множин

1.4. Узагальнення операцій. Подвійність

1.1. Основні поняття і завдання множин

Визначення. Під множиною розуміється об'єднання визначених, відмінних один від одного об'єктів (реальних чи уявлюваних), що називають елементами множини в їхній сутності.

Приклад. А={ 1,2,а,b} - коректно, В={ а,b,c,b} - некоректно.

Загальне позначення множин - фігурні дужки {...}, усередині яких задаються елементи множин. Конкретні множини позначаються великими літерами А, В₄, С_і,..., елементи множин позначаються рядковими латинськими літерами a, b₄, сі....

Запис mÎM означає висловлення «m є елементом множини М» чи «m належить множині М». Запис mÏM означає заперечення висловлення mÎM.

Запис М₁ÍМ₂ означає висловлення «кожен елемент множини М₁ є елементом множини М₂», чи «M₁ є підмножиною множини М₂, а М₂ – надмножиною множини М₁», чи «M₁ міститьться в М₂».

Запис М₁ËМ₂ - заперечення висловлення М₁ÍМ₂.

Запис М₁=М₂ означає висловлення «M₁ÍM₂ і М₂ÍМ₁» чи «множини М₁ і М₂ рівні (еквівалентні)».

Запис М₁¹М₂ - заперечення висловлення М₁=М₂.

Запис М₁ÌМ₂ еквівалентний висловленню «M₁ÍM₂ і М₁¹М₂» чи «M₁ є власною підмножиною множини М₂». Невласні множини в цьому випадку - сама множина М₂ і множина Æ - єдина множина, що не містить елементів - порожнє М.

Можна вважати, що всі розглянуті множини є підмножинами деякого універсуму U (для цілих чисел - нескінченність).

Визначення. Множина, елементами якої є всі підмножини множини М, називається множиною підмножин, чи множиною-ступенем, чи булеаном множини М і позначається як Р(М) чи В(М).

Приклад. М={1,2,3}, P(M)={Æ, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}}.

Запис |М| означає число елементів множини М, |Р(М)|= 2^|М|.

Завдання множин здійснюється трьома основними способами:

1. Приклад: Перерахування всіх елементів, що входять у множину.

Приклад. А={а₁, а₂, а₃ }, B={1, 2, b, c}, C={а_і}₁ ³

2. Завданням характеристичної властивості, що виділяє елементи даної множини серед елементів, що зазначені іншим множинам.

Приклад. N={n|nÎZ і n>0}, М={mÎM|m=n² і nÎN}

3. Описом процедури, що породжує, із зазначенням множин, що пробігають параметри цієї процедури.

Приклад. М={n²|nÎN}, C ={8х₁+14х₂+32х₃|х₁, х₂, х₃ÎZ}.

З визначення рівності множин і способів завдання їх випливає, що порядок елементів у множинах несуттєвий.

Для інтерпретації множин і операцій над ними використовуються геометричні фігури - кола Ейлера і діаграми Венна (рис. 1.1.).

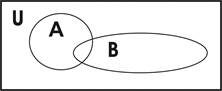
Рис. 1.1. Кола Ейлера

1.2. Операції над множинами. Формули. Тотожності

Нові множини породжуються в результаті застосування операцій до існуючих множин.

Об'єднанням множин М₁ і М₂ називається множина М₁ÈM₂={m|mÎM₁ чи mÎM₂}.

Перетином множин М₁ і М₂ називається множина М₁ÇM₂={m|mÎM₁ і mÎM₂}.

Множини М₁ і М₂ називаються диз'юнктними, якщо М₁ ÇM₂=Æ.

Різниця множин М₁ і М₂ - це множина М₁\М₂={m|mÎM₁ і mÏM₂}.

Симетричною різницею множин М₁ і М₂ називається множина
М₁-М₂= {m|mÎM₁\M₂ чи mÎМ₂\М₁}.

Якщо М₁ÍM₂, то різниця М₂\М₁ називається доповненням
множини М₁ у множині М₂. Зокрема, ` М = U\M - доповнення множини М в універсумі чи просто доповнення множини М. Інше позначення доповнення множини - ùМ.

Приклад. A={1,2, 3, 4}; B={3, 4 5}; З ={1, 3}; AÈB={1, 2, 3, 4, 5}; AÇB={3, 4}; A\З ={2, 4}; A\B={1, 2}; B\A={5}; A-B={1,2,5}.

Теорема. Будь-які дві множини А і В можуть знаходитися в одному з п'яти станів: 1)А=В; 2)АÌВ; 3)АÉВ; 4)АÇВ=Æ; 5)А\В ¹Æ і В\А¹Æ і АÇВ¹Æ

Завдання нових множин за допомогою ідентифікаторів, операцій і дужок, тобто завдання за допомогою формул називається аналітичним.

Для операцій над множинами справедливі закони (тотожності):

1. AÈB=BÈA; AÇB=BÇA; комутативність

2. AÈ(BÈЗ)=(AÈB)ÈЗ; AÇ(BÇЗ)=(AÇB)ÇC; асоціативність

3. AÈ(BÇC)=(AÈB)Ç(AÈC); AÇ(BÈC)=(AÇB)È(AÇC);

дистрибутивність

4. AÈÆ=A; AÈU=U;
AÇÆ=Æ; AÇU=A;
`Æ=U; `U=Æ; властивості границь

5. AÈ`A=U; AÇ`A=Æ; доповнення

6. AÈA=A; AÇA=A; ідемпотентність

7. AÈ(AÇB)=A; AÇ(AÈB)=A; поглинання

8. AÈ(`AÇB)=AÈB; AÇ(`AÈB)=AÇB;
(AÇC)È(BÇ`C)=(AÇC)È(BÇ`C)È(AÇB);
(AÈC)Ç(BÈ`C)=(AÈC)Ç(BÈ`C)Ç(AÈB) Блейка-Порецького

9. (AÇB)È(`AÇB)=B; (AÈB)Ç(`AÈB)=B склеювання

10. ù(AÇB)=`AÈ`B; ù(AÈB)=`AÇ`B; деМоргана

11. Якщо АÈB=U і AÇB=Æ то A=`B

12. ù ùA=A; інволютивність

13. A\B=AÇ`B

14. A-B=B-A; комутативність

15. A-(B-C)=(A-B)-C; асоціативність

16. A-Æ=Æ-A=A; A-U=U-А=`A; властивості границь

17. AÍB, якщо і тільки якщо АÈB=B і AÇB=A і AÇ`B=Æ

18. A=B, якщо і тільки якщо A-B=.

1.3. Доведеннятотожностей. Булева алгебра множин

Для доведення тотожностей використовується універсальний метод, в основу якого покладене визначення рівності (еквівалентності) двох множин. Кожне з доведень складається з послідовності тверджень вигляду “якщо Р, то Q”, записується як “PÞQ” і що читаються як “з R випливає Q”. Отже, якщо існує послідовність тверджень Р, Р₁, Р₂, Р₃,..., Р_n, Q така, що з Р випливає Р₁, з Р₁ випливає Р₂,…з Р_n випливає Q, то існує доведення, що “з Р випливає Q”, тобто RÞQ.

Приклад. D=AÇ(BÈС) = (AÇB)È(AÇС)=E

а) Доведемо, що DÍE. Якщо dÎD, то dÎA і dÎ(BÈC), чи отже, (dÎA і dÎB), чи (dÎA і dÎC). Це значить, що dÎAÇB чи dÎAÇC), тобто dÎ(AÇB)È(AÇC), що записується як dÎE. Тобто, DÍE.

б) Доведемо, що ЕÍD. Якщо еÎE то еÎ((AÇB) чи (AÇС)), отже еÎA і еÎB) чи еÎA і еÎC. Це значить, що еÎA і еÎ(BÈC) тобто еÎD. Тобто, ЕÍD. Отже, D=Е.

Для доведення тотожностей можуть бути використані доведені раніше тотожності.

Приклад. AÈ(AÇB)=A; AÈ(AÇB) = (AÇU)È(AÇB) = AÇ(UÈB) =
= AÇU = A.

Для кожної множини М, булеан У(М) замкнутий щодо операцій È,Ç,\,-,ù, тобто для всяких М₁, М₂ÎB(M) множини, одержувані в результаті виконання операцій М₁ÈM₂, M₁ÇM₂, M₁\M₂, M₂\M_1,, M₁-M₂, `M<sub>1</sub>,`M₂ є елементами булеана В(М).

Булеан B(М) разом з (булевими) операціями на ньому утворюють так звану (булеву) алгебру множин. Кожна підмножина M’ булеана В(М) замкнута відносно (булевих) операцій, містить як множини, що є підмножинами кожної множини з M’, так і множини, що містять як підмножини кожну множину з M’. Таким чином, M’ з (булевими) операціями також виявляється (булевою) алгеброю.

1.4. Узагальнення операцій. Подвійність

Завдякі властивості асоціативності об'єднання, Перетин і симетрична різниця довільних сімей множин можуть бути записані без пріоритетних дужок.

1. М₁ÈM₂ȼÈМ_n=È{М_і|1£ і £ n}={m| існує і, де 1£і£n, таке, що mÎM_і}.

2. М₁ÇM₂ǼÇM_n=Ç{M_і|1£ і £ n}={m| для кожного і., де 1£ і£n, виконане mÎM_і}.

3. М₁-M₂-¼-M_n=-{M_і|1 £ і £ n }={m| існує і єдино і, де 1£і£n, таке, що mÎM_і}.

Ці визначення узагальнюються на випадок, коли множини М_і задані як елементи деякої сім'ї множин М и потрібно виконання деякої додаткової умови В:

È{M_і|M_іÎM і М_і задовольняє умову В}.

Приклад. È{M_і|M_іÎB(Z) і M_іÇN₀=Æ} - множина усіх від'ємних цілих чисел.

Замість È{M_і|іÎN} використовується запис ÈM_і. Аналогічно - для ¢¢Ç¢¢ і ¢¢-¢¢.

Перші вісім тотожностей представлені парами подвійних (дуальних) співвідношень, одне з яких виходить заміною в іншому символів “È” на “Ç” і “Ç” на “È”, а також Æ на U і U на Æ. Відповідні пари символів È, Ç і Æ, U називаються подвійними (дуальними).

Принцип подвійності: При заміні в будь-якій теоремі (тотожності, формулі) вхідних у неї символів дуальними одержимо новий вираз, що також є теоремою (тотожністю, формулою).

Тотожності 9, 11 не змінюються при заміні символів дуальними і називаються самоподвійними. Принцип подвійності поширюється на “\”, -, а також на вираження, що включають знаки “Ì” і ”É”, які при переході до дуальних виражень заміняються на знаки відповідно “É” і “Ì”.

Різні вираження алгебри множин можна спрощувати чи перетворювати до зручного вигляду за допомогою тотожних перетворень, тобто послідовності застосувань відповідних властивостей (тотожностей) операцій над множинами.

Контрольні запитання

1. Що є множина, фактор-множина, порожня множина і універсум?

2. Які способи завдання множин існують?

3. Які операції діють над множинами?

4. Як можуть співвідноситися дві множини?

5. Які тотожності для операцій над множинами існують?

6. Які способи доведення тотожностей існують?

7. Для яких операцій можливе узагальнення і яке саме?

8. У чому полягає принцип подвійності?

Спісок літератури: