Список літератури. 1. Коршунов Ю.М. Математические основы кибернетики

Основна

1. Коршунов Ю.М. Математические основы кибернетики. – М.: Энергоатомиздат, 1987. - С.48-62.

2. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2001. - С.33-41.

3. Сигорский В.П. Математический аппарат инженера. – К.: Техника, 1975. - С.106-115.

Додаткова

4. Кук Д., Бейз Г. Компьютерная математика. – М.: Наука, 1990. - С.35-43, 68-73.

5. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра, языки, программирование. – К.:Наукова думка, 1989. - С.35-50.

Для практичних занять

6. Методичні вказівки і завдання до контрольних робіт з дисципліни «Основи дискретної математики» для студентів очної та заочної форм навчання фахів 6.0804, 6.0915 / О.М. Мартинюк. – Одеса: ОНПУ, 2001. – С.10-13.

Лекція 5. Відношення

Вступ

Лекція має за мету висвітлити початкові поняття з відношень і графіків відношень. Розглянуті визначення і n-арність відношень, типові відношення, множинні операції об’єднання, перетин, різниці, симетричної різниці, декартова добутку. Звернено повагу на ототожнення відношень і їх графіків, що часто використаємо, а також асоціативність декартова добутку відношень.

Лекція містить два підрозділи:

5.1. Основні поняття відношень

5.2. Множинні операції відношень

5.1. Основні поняття відношень

Визначення. Під n-арним відношенням чи n-відношенням rⁿ на множинах А₁, А₂,..., А_n розуміється закон (характеристична властивість), що виділяє в декартовому добутку А₁´A₂´...´A_n деяку підмножину rⁿ_A1,...,AnÍA₁´A₂´...´A_n, що називана (n-вимірним) графіком відношення rⁿ. Якщо А₁=А₂=...=А_n=A, то говорять про n-відношення rⁿ на множині А з графіком rⁿ_AÍAⁿ.

Відношення, як і відповідності, часто позначають грецькими літерами, з індексами чи без них, і спеціальними символами =, £, ³, <, >.

Часто поняття n-відношення ототожнюється з його графіком, тобто під n-відношенням rⁿ на множинах А₁, А₂,..., А_n розуміється сама підмножина:

rⁿ_A1,¼,AnÍA₁´A₂´¼´A_n.

Якщо a=(а₁, а₂,..., а_n)Îrⁿ_{1,.., An}, де а_jÎA_j, j=1, 2,..., n, то говорять, що елементи а₁, а₂,..., а_n знаходяться у відношенні rⁿ: rⁿ(a₁, a₂,..., a_n), так що позначення (а₁, a₂,..., a_n)Î rⁿ і rⁿ(a₁, a₂,..., a_n) рівносильні.

Визначення. Послідовність a=(а₁, a₂,..., a_n)Îrⁿ_A1,...,An називається елементом чи вектором n-відношення rⁿ. Відношення, графіки яких містять скінченні множини векторів, називають скінченними
n-відношеннями. Якщо rⁿ_1,...,An=Æ, то rⁿ- порожнє n-відношення (Ùⁿ), якщо rⁿ_{1,..., An}=A₁´A₂´¼´A_n, то rⁿ- універсальне n-відношення (Úⁿ).

Тому що n-відношення rⁿ можна розглядати як підмножини декартова добутку А₁´A₂´¼´А_n, існують різні способи завдання
n-відношень, аналогічні способам завдання множин. Так графік rⁿ_1,...,An зручно задавати матрицею, рядками якої є вектори відношення rⁿ.

Приклад. rⁿ_{1,..., An}={a ^j=(a₁ ^j, a₂ ^j,..., a_n ^j|j=1, 2,..., r} - множина усіх векторів, графік у матричній формі

rⁿ_{A1,..., An}= a₁ ^j1 a₂ ^j1... a_n ^j1

a₁ ^ji2 a₂ ^j2... a_n ^j2

..................................

a₁ ^jr a₂ ^jr... a_n ^jr

Відношення r¹ на множини А називають унарними, відношення r² на А, В - бінарними, відношення r³ на А, В, С - тернарними і т.д.

Унарне відношення r¹ на множини А є характеристичною властивістю деякої підмножини r¹_АÎA - графіка даного відношення, таким чином, множина всіх унарних відношень на А збігається з множиною всіх підмножин множини А. Якщо ½А½=n, то число унарних відношень на А дорівнює 2ⁿ.

Лема. Будь-якому n-відношенню r ⁿ на множинах А₁, А₂,..., А_n відповідає унарне відношення r¹ на множини А₁´A₂´¼´A_n таке, що виконується r¹(a) тоді і тільки тоді, коли для відношення виконується r ⁿ(a₁ ^і, a₂ ^і..., a_n ^і), де a=(a₁ ^і, a₂ ^і,..., a_n ^і) - довільний вектор відношення r ⁿ.

Бінарне відношення r на множинах А і В визначається графіком r_A,BÍA´B. Якщо елементи аÎA і bÎB знаходяться у відношенні r, то поряд з позначеннями (а, b)Îr_A,B і r(a, b) використовується й аrb.

Приклад. а)А={2, 3, 5} r_A,B= 2 2

B={2, 3, 4, 5, 6} 2 4

3 3

3 6

5 5

б) Таблиця 5.1

rA,B
	х		х		х
		х			х
				х

в)

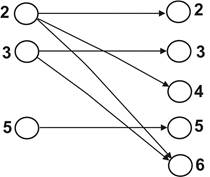
Рис. 5.1. Бінарне відношення r_A,B

Графік тернарного відношення r³ має вигляд r³_A,B,CÍA´B´С.

З кожною бінарною операцією F(х,у), зокрема з арифметичними операціями “+”, ”-”, ”×”, ”:” і іншими, може бути зв'язане тернарне відношення j³ таке, що j³(х, у, z) тоді і тільки тоді, коли F(х, у)=z.

Найбільше часто вживаються бінарні відношення (графіки на площині).

Якщо для бінарного відношення r²_А1,А2ÍА₁´A₂ множини А₁ і А₂ рівні А, то говорять, що визначено відношення на множині А, тобто r²_А.

Визначення. Відношення на множині А називається

а) повним, якщо r²_А=А²;

б)порожнім і позначається 0_А, якщо r²_А=Æ;

в) відношенням рівності і позначається Е_А, якщо і тільки якщо r²_А містить всі можливі пари з однаковими компонентами;

г) відношенням нерівності, якщо r²_А не містить ні однієї пари з однаковими компонентами.

5.2. Множинні операції відношень

Вивчення n-відношень на множинах А₁, А₂,..., А_n можна зв'язати з вивченням їхніх графіків, тобто підмножин А₁´A₂´¼´A_n. На множини
n-відношень поширюються множинні операції “È”, ”Ç”, ”\”, ”-”, ”ù” і множинні відношення включення “Í”, тобто з rⁿ _{A1, A2,..., An} Ísⁿ _{A1, A2,..., An}- включення графіків випливає включення відношень rⁿÍsⁿ.

Визначення. Об'єднання відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ È s ⁿ з графіком q ⁿ _{A1, A2,..., An}=r ⁿ _{A1, A2,..., An} È s ⁿ _{A1, A2,..., An}.

Визначення. Перетин відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ Ç s ⁿ з графіком q ⁿ _{A1, A2,..., An}=r ⁿ _{A1, A2,..., An} Ç s ⁿ _{A1, A2,..., An}.

Визначення. Різниця відношень r ⁿ і s ⁿ - то відношення
q ⁿ=r ⁿ \ s ⁿ з графіком q ⁿ _{A1, A2,..., An}=r ⁿ _{A1, A2,..., An} \ s ⁿ _{A1, A2,..., An.}

Визначення. Симетрична різниця відношень r ⁿ і s ⁿ - це відношення
q ⁿ=r ⁿ - s ⁿ з графіком q ⁿ _{A1, A2,..., An}=r ⁿ _{A1, A2,..., An} - s ⁿ _{A1, A2..., An}.

Визначення. Відношення`r <sup>n</sup> називається доповненням відношення r<sup>n</sup>, якщо a Î r <sup>n</sup> <sub>A1, A2,..., An</sub> тоді і тільки тоді, коли`a Ï r ⁿ _{A1, A2,..., An}

Приклад. Для бінарних відношень <, =, £, ³, > справедливо

£_N = <_N È =_N; =_N = £_N Ç ³_N; <_N =`³_N.

Нехай rⁿ - відношення на множинах А₁, А₂,..., А_n, а s^m - відношення на множинах Аn₊₁,..., A_n+m.

Визначення. Декартів добуток відношень r ⁿ і s ^m - це відношення
q ^n+m=r ⁿ´s ^m, графік якого має вигляд

q ^n+m _{A1, A2,..., An+m}=r ⁿ _{A1, A2,..., An} ´ s ^m_{An+1,..., An+m}.

Слід мати на увазі, що в цьому випадку допускається асоціативність декартова добутку.

Приклад. Нехай А₁={0, 1, 2}, A₂={a, b}, A₃={b, c, d} і a ³, b ³ – відношення:

a ²_{A1, A2}= 0 a b ³_{A1, A2, A3}= 0 a b

1 b 1 b c

1 b d

Тоді відношення g ⁵=a ²´b ³ визначається графіком:

g⁵_{A1, A2, A3 A4, A5}= 0 a ´ 0 a b = 0 a 0 a b

1 b 1 b c 0 a 1 d c

1 b d 0 a 1 b d

1 b 0 a b

1 b 1 b c

1 b 1 b d

Контрольні запитання

1. Що є n-арне відношення?

2. Як можна зіставити n-арному відношенню унарне відношення?

3. Як можна зіставити бінарної операції тернарне відношення?

4. Які способи завдання відношень існують?

5. Які типові відношення існують?

6. Які множинні операції для відношень?

7. Що є асоціативністю декартова добутку відношень?