Рассмотрим возможность представления произвольной булевой функции в виде формулы из элементарных функций. Так, теоремы 1 и 2 доказывают возможность такого представления в виде формулы, содержащей только функции дизъюнкции, конъюнкции и отрицания.
Теорема 1. Произвольную булеву функцию f (x1,x2...,xn) можно представить в виде
s=(1,...,1)
f (x1,x2...,xn) = ٧ f (s1,s2...,sn) х1s1 х2s2 ... хnsn, (4)
s=(0,...,0)
где si Î {0, 1}, xi0 =`xi, xi1 = хi , s = (s1,...,sn) и дизъюнкция берётся по всем n-мерным наборам из нулей и единиц.
Доказательство. Покажем, что левая и правая части соотношения (4) совпадают. Произвольный набор a = (a1, a2,..., an),[Ò2] где каждое ai Î {0,1}, подставим в соотношение (4). В левой части получим f (a1,a2,..,an), а в правой части
s=(1,...,1)
٧ f(s1,s2,...,sn) a1s1a2s2...ansn = f(a1,a2,...,an) a1a1a2a2...anan =
s=(0,...,0)
 = f (a1,a2,...,an).
= f (a1,a2,...,an).
Равенства в правой части вытекают из свойств конъюнкции, дизъюнкции и из того, что хs = 1 Û x = s.
Если f (x1, x2,...,xn) ≢ 0, то соотношение (4) можно переписать в форме
f (x1, x2...,xn) = ٧ х1s1 х2s2×××хnsn (5)
по всем s
f (s)=1
Эта форма называется совершенной дизъюнктивной нормальной формой (совершенной ДНФ) функции f (x1,x2,...,xn).
Построение совершенной ДНФ из табличного задания функции производится следующим образом. Для каждого набора s = (s1,...,sn) такого, что f (s1,...,sn) = 1, составляется выражение х1s1×××хnsn и затем все такие конъюнкции соединяются знаком дизъюнкции. Например, для функции сложения по модулю два совершенная ДНФ имеет вид
х1 Å х2 =`х1х2 ٧ х1`x2 .
Теорема 2. Произвольную булеву функцию f (x1,x2,...,xn) можно представить в виде
s=(1,...,1)
f (x1,x2,...,xn) = ٨ (f (s1,s2...,sn) ٧ х1`s1 ٧ х2`s1 ٧...٧ хn`sn), (6)
s=(0,...,0)
где si = {0,1}, xi0 = `xi, xi1 = хi, s = (s1,...,sn) и конъюнкция берётся по всем n-мерным наборам из нулей и единиц.
Доказательство. Из свойства булевой функции (закон двойного отрицания) имеем f (x1,...,xn) = 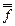 (x1,...,xn).
(x1,...,xn).
Для функции`f (x1,...,xn) по теореме 1 существует представление в виде
s=(1,...,1)
`f (x1,x2,...,xn) = ٧ `f (s1,s2,...,sn) х1s1х2s2...хnsn, тогда
s=(0,...,0)
 s= (1,...,1)
s= (1,...,1)
f (x1,x2,...,xn) = ٧ `f (s1,s2,...,sn) х1s1х2s2...хnsn =
s=(0,...,0)
s=(1,...,1)
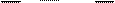 = ٨ (f (s1,s2,...,sn) ٧ x1s1 ٧ x2s2 ٧...٧ xnsn), что следует из закона
= ٨ (f (s1,s2,...,sn) ٧ x1s1 ٧ x2s2 ٧...٧ xnsn), что следует из закона
s=(0,...,0)
де Моргана.  Заметим также, что xisi = xi`si. Следовательно,
Заметим также, что xisi = xi`si. Следовательно,
s=(1,...,1)
 f (x1,х2,...,xn) = ٨ (f (s1,s2,...,sn) ٧ х1`s1 ٧ х2`s2 ٧...٧ хn`sn)
f (x1,х2,...,xn) = ٨ (f (s1,s2,...,sn) ٧ х1`s1 ٧ х2`s2 ٧...٧ хn`sn)
s=(0,...,0)
Если f (x1,x2,...,xn) ≢ 1, то соотношение (6) можно переписать в форме
f(x1,x2,...,xn) = ٨ (х1`s1 ٧ х2`s2 ٧...٧ хn`sn ). (7)
по всем s,
f(s)=0
Эта форма называется совершенной конъюнктивной нормальной формой (совершенной КНФ) функции f (x1,x2,...,xn).
Построим совершенную КНФ функции х1 Å х2 (табл. 3.5):
х1 Å х2 = (х1 ٧ х2) (`х1 ٧ `х2).
Вывод. Булеву функцию любого числа переменных можно построить из функций одной или двух переменных. Средством такого построения является суперпозиция булевых функций, то есть подстановка одних булевых функций вместо переменных в другие булевы функции.
 2015-06-28
2015-06-28 289
289








