1) Откроем таблицы Excel. Внесем выборочные данные по всем округам в столбец А (диапазон А2:А87). В ячейках D2:D5 вычислим характеристики выборки: объем выборки n (функция СЧЁТ), среднее значение х ср (функция СРЗНАЧ), выборочную дисперсию s2 (функция ДИСПР), исправленную выборочную дисперсию s2испр (функция ДИСП). Внесем также значение доверительной вероятности Р=0,9.
Поскольку объем генеральной совокупности неизвестен, а выборка считается большой, мы должны использовать формулу стандартной ошибки для среднего большой выборки с повторным отбором. Однако в этом случае проще сразу вычислить предельную ошибку при помощи функции ДОВЕРИТ:
Рисунок 2.1. Пример. Расчет предельной ошибки среднего большой выборки
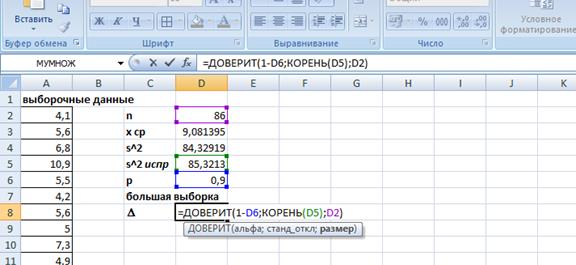
Полученное значение D=1,63835. Таким образом, доверительный интервал для среднего уровня безработицы 9,08±1,64.
2) Применим теперь формулу ошибки для малой выборки. Вычислим коэффициент доверия t, введя в ячейку G8 формулу
=СТЬЮДРАСПОБР(1-D6;D2-1).
Предельную ошибку вычисляем в ячейке G9:
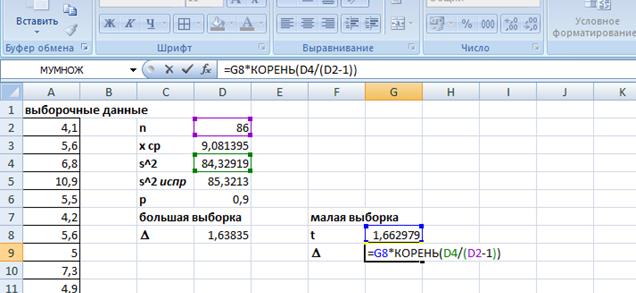
Полученное значение D=1,656403. Таким образом, доверительный интервал для среднего уровня безработицы 9,08±1,656.
Видим, что предельная ошибка, вычисленная по формуле для малой выборки несколько больше, чем по формуле для большой выборки, но различие в данном случае невелико. С ростом объема выборки это различие уменьшается.
 2015-06-28
2015-06-28 559
559







