Теорема Фон–Неймана

В матричной игре существует пара 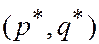смешанных стратегий, таких что

1. 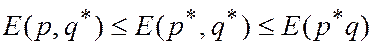, " p Î P_m, q Î Q_n.

2. a = b = .

Доказательство. Сначала покажем, как представить задачу о выборе
наилучших стратегий в виде ЛП, а затем докажем теорему.

Первый игрок: a (p) ® max

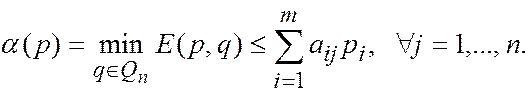
Пусть u_i = p_i / a (p), i = 1,…, m, в предположении a (p) > 0.

Тогда u_i ³ 0, i = 1,…, m, и 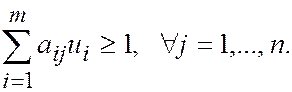Заметим, что 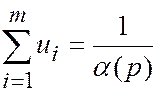и задача a (p) ® max может быть записана следующим образом:

,

.

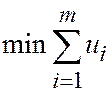
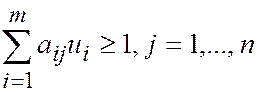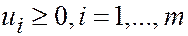Аналогичным образом получаем задачу второго игрока:

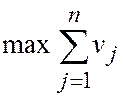
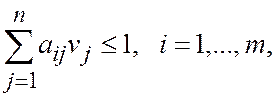
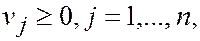
где v_j = q_j / b (q), j = 1,…, n. Полученные задачи являются взаимодвойственными. Пусть 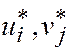— оптимальные решения этих задач.

Положим 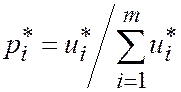, 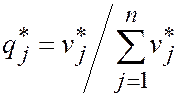. Из второй теоремы двойственности следует, что

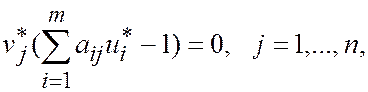
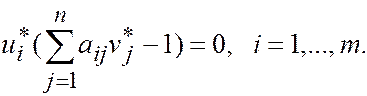
Просуммировав, получим

.

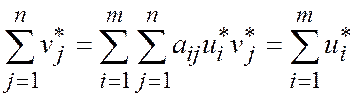Поделим на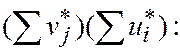

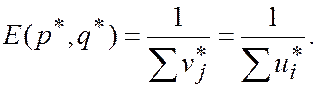
Теперь докажем первое утверждение теоремы:

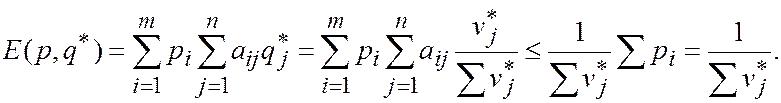
Аналогично

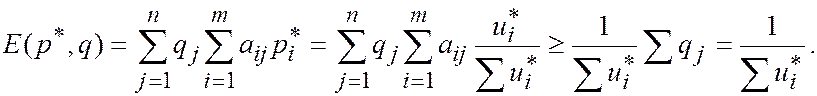
т.е.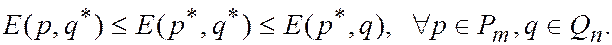

Докажем второе утверждение теоремы.

Из предыдущего неравенства имеем:

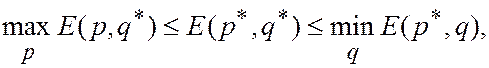
т.е.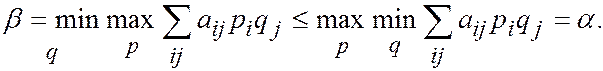

Но по лемме a £ b Þ a = b =

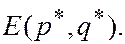
Дилемма заключенных

Два преступника пойманы за совершение преступления.
У следствия не хватает доказательств их виновности и преступникам предлагают сделку:

Если сознаешься и подтвердишь участие товарища в преступлении, то выйдешь на свободу, а товарищ получит 7 лет лишения свободы.

Преступники сидят в разных камерах и не могут общаться, но они знают, что каждому сделано такое предложение.

Если оба преступника сознаются, то каждый получит 5 лет.

Если оба не сознаются, то каждый получит по 1 году.