 Предметом исследований в теории игр являются модели и методы принятия решений в ситуациях, где участвуют
Предметом исследований в теории игр являются модели и методы принятия решений в ситуациях, где участвуют
несколько сторон (игроков). Цели игроков различны, часто противоположны. Мы будем рассматривать только игры двух лиц с противоположными интересами.
Игра состоит из последовательности ходов. Ходы бывают личные и
случайные.(В шахматах все ходы личные. Рулетка содержит случайный ход).
Результаты ходов оцениваются функцией выигрыша для каждого игрока. Если сумма выигрышей равна 0, то игра называется игрой с нулевой суммой
(преферанс). Будем рассматривать только такие игры.
 Стратегией называется набор правил, определяющих
Стратегией называется набор правил, определяющих
поведение игрока, т.е. выбор хода.
Оптимальной стратегией называют такую стратегию, при которой достигается максимальный ожидаемый
средний выигрыш при многократном повторении игры.
Матричные игры — это игры, где два игрока играют в игру с нулевой суммой, имея конечное число «чистых» стратегий: {1,…, m } и {1,…, n } и " (ij) задан платеж aij второго игрока первому. Матрица (aij) задает выигрыш первого
игрока и проигрыш второго, aij ≷ 0!
Игра в орлянку.
Игроки выбирают ходÎ{ орел, решка }. Если ходы совпали, то выиграл первый, иначе второй.
 II игрок II игрок | орел | решка |
| I игрок | ||
| орел | – 1 | |
| решка | – 1 |
Прорыв обороны. Первый игрок выбирает систему зенитного вооружения. Второй игрок выбирает самолет. Элементы aij задают вероятность поражения самолета j системой i. Цель второго игрока — прорвать оборону.
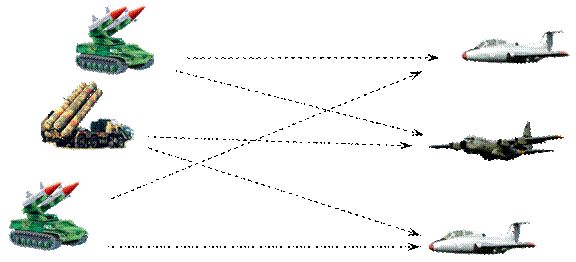
| Самолеты | |||
| Зенитки | 0,5 | 0,6 | 0,8 |
| 0,9 | 0,7 | 0,8 | |
| 0,7 | 0,5 | 0,6 |
В первом примере все ходы одинаково плохи или хороши. Во втором примере ход (2, 2) в некотором смысле лучший для обеих сторон: если взять самолет 2, то зенитка 2 — лучшая для первого игрока; если взять зенитку 2, то самолет 2 лучший для второго. В матрице есть седловая точка!
Определение. Седловой точкой матрицы (aij) называют пару (i 0 j 0) такую, что
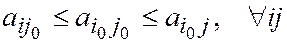 .
.
 2015-06-28
2015-06-28 1333
1333







