Принцип минимакса (осторожности)

Предположим, что противник всеведущ и угадывает все ходы! Первый игрок предполагает, что второй все знает и для хода i первого игрока выберет j (i):
a_{ij ( i )} £ a_ij," j = 1,…, n. Обозначим 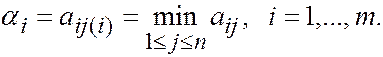Тогда лучшей
стратегией для первого игрока является выбор i ₀ такой, что

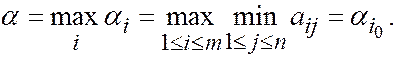
Величину a назовем нижней ценой игры в чистых стратегиях.

Второй игрок из соображений осторожности считает, что первый " j выберет i (j) так, что a_{i ( j ) j} ³ a_ij, " i, т.е. и выбирает j с минимальным b_j, т.е.

.

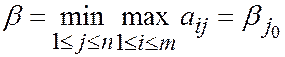Величину b назовем верхней ценой игры в чистых стратегиях.

Пример 1. a = –1, b = +1, a £ b

Пример 2. ,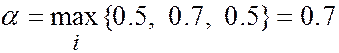

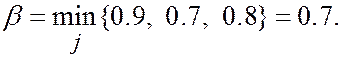
Лемма. Для любой функции f (x, y), x Î X, y Î Y, справедливо неравенство

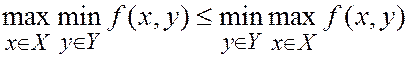
в предположении, что эти величины существуют.

Доказательство. Введем обозначения:

,

.

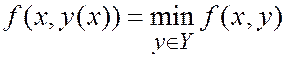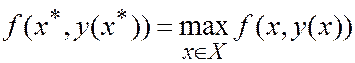Тогда

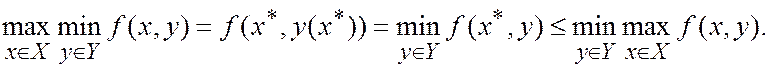
Теорема. Необходимым и достаточным условием равенства верхней и нижней цен игры в чистых стратегиях является существование седловой точки
в матрице (a_ij).

Доказательство. Необходимость. Пусть a = b. По определению

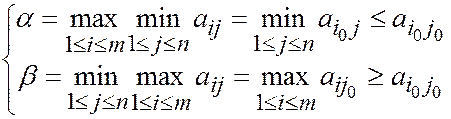
т.е. 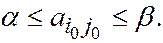Так как a = b, то 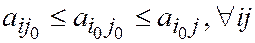, т.е. является седловой точкой.

Достаточность. Пусть седловая точка (i ₀ j ₀) существует, т.е.

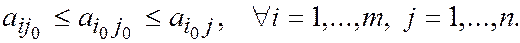
Тогда 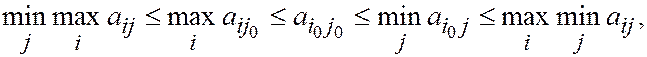но по лемме верно обратное, т.е. 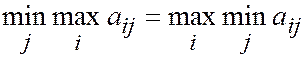. Следовательно a = b.