Умножение вектора на число. Произведением вектора 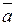на число λ называется вектор 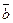=λ , коллинеарный вектору

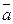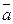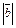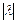
Произведением вектора на число λ называется вектор =λ , коллинеарный вектору и имеющий длину = 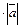. Вектор 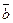одинаково направлен с вектором 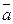при λ>0 и противоположно 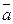при λ<0. Если λ=0, то λ = .

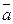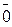Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: 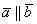, при этом возможна детализация: 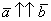(векторы сонаправлены) или 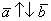(векторы направлены противоположно).

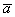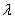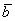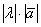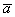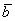Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при 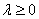и противоположно направлены при .

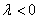Правило умножения вектора на число легче понять с помощью рисунка:

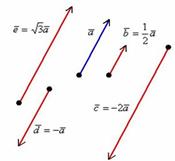
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».