Скалярным произведением векторов 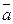 и
и 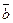 называется число, равное произведению длин этих векторов на косинус угла φ между ними. Обозначается скалярное произведение векторов
называется число, равное произведению длин этих векторов на косинус угла φ между ними. Обозначается скалярное произведение векторов 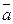 и
и 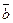 так:
так: 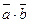 или (
или (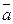 ,
, 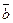 ). Следовательно:
). Следовательно: 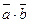 =
= 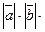 cosφ, отсюда cosφ=
cosφ, отсюда cosφ= 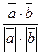 .
.
Скалярным произведением двух векторов, заданных в координатной форме, называется число равное сумме произведений одноименных координат.
Пусть на плоскости OXY заданы векторы 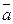 =(a1, a2) и
=(a1, a2) и 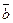 =(b1, b2), их скалярное произведение
=(b1, b2), их скалярное произведение 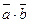 =a1b1+a2b2.
=a1b1+a2b2.
Аналогично находится скалярное произведение векторов: 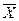 =(x1, x2,…, xn) и
=(x1, x2,…, xn) и 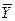 =(y1, y2,…, yn).
=(y1, y2,…, yn).
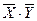 =x1y1+x2y2+…+xnyn.
=x1y1+x2y2+…+xnyn.
Свойства скалярного произведения:
- 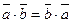 (переместительный закон),
(переместительный закон),
- 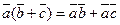 (распределительный закон),
(распределительный закон),
- 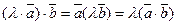 (сочетательный закон по отношению к скалярному множителю λ),
(сочетательный закон по отношению к скалярному множителю λ),
- 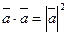 или
или 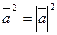 , откуда
, откуда 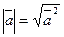 ,
,
- если 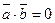 , то
, то 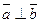 или один из векторов нулевой.
или один из векторов нулевой.
Угол φ между векторами 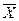 =(x1, x2,…, xn) и
=(x1, x2,…, xn) и 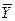 =(y1, y2,…, yn) найдем по формуле:
=(y1, y2,…, yn) найдем по формуле:
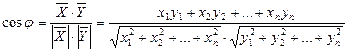 .
.
Пример 1. Найти скалярное произведение векторов 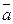 =(-1; 0; 7) и
=(-1; 0; 7) и 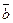 =(-3; 1; 5).
=(-3; 1; 5).
Решение. 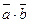 =-1(-3)+0∙1+7∙5=38.
=-1(-3)+0∙1+7∙5=38.
Пример 2. Найти угол φ между векторами 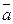 =(0; 6; -2) и
=(0; 6; -2) и 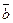 =(2; 2; -8).
=(2; 2; -8).
Решение. Угол φ найдем используя формулу:
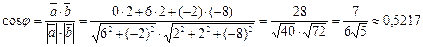
 2015-06-28
2015-06-28 417
417








