2015-06-28
1347
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы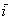 
и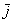 
:
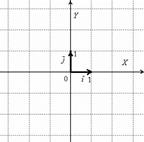
Векторы 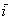и 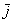ортогональны. Ортогональны = Перпендикулярны. Рекомендую потихоньку привыкать к терминам: вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.
Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например: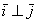 
.
Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например: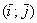 
. Координатные векторы нельзя переставлять местами.
Любой вектор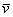 
плоскости единственным образом выражается в ви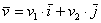де:
, где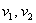 
– числа, которые называются координатами вектора в данном базисе. А само выражение 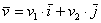называется разложением вектора 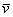по базису .
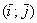Задан ортонормированный базис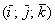 
трехмерного пространства и прямоугольная система координат, единичные векторы 
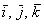данного базиса попарно ортогональны: 
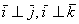и 
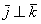. Ось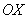 
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства.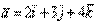 
|
|
|
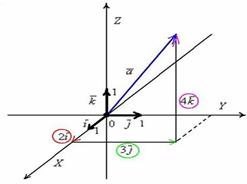
Любой вектор 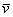трехмерного пространства можно единственным способом разложить по ортонормированному базису :
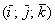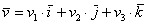, где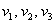 
– координаты вектора 
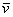(числа).
Базисные векторы записываются следующим образом:
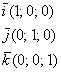
4. Простейшие задачи аналитической геометрии.
Действия с векторами в координатах
