Координаты векторов на прямой

Рассмотрим прямую, на которой введена система координат для точек (ось). Рассмотрим вектор 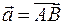на этой оси. Координатой этого вектора назовем число, равное 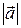, если направление вектора 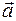совпадает с направлением оси или равное 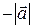в противном случае. (Координату нулевого вектора полагаем равной нулю.) Запись 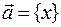означает, что вектор 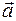имеет координату 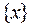. Если известны координаты точек 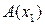и 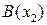, то очевидно, что .

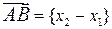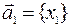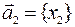Вектор на оси выражает смещение по оси, его координата – числовую величину этого смещения. Легко показать, что если и , а 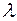- число, то 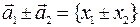, и 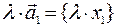, то есть при сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координата умножается на это число.