Умножение вектора на число

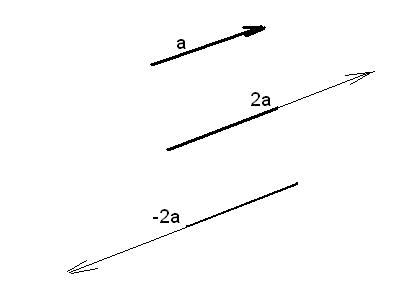
При умножении вектора 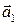на число 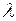мы получаем коллинеарный ему вектор 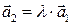. В случае 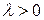вектор 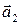направлен в ту же сторону, что и вектор 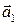, а в случае 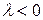вектор 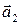направлен в противоположную сторону. В обоих случаях длина вектора 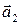должна быть .

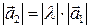Нулевой вектор при умножении на любое число остается нулевым. При умножении любого вектора на число ноль он становится нулевым:

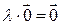
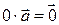
Итак, во всех случаях выполнено равенство .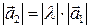

Мы обозначаем умножение вектора на число точкой, так же как и умножение чисел (но это другая операция). Это удобно, и не вызывает путаницы.

Нетрудно проверить, что .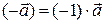

Линейные операции над векторами обладают следующими, легко проверяемыми свойствами:

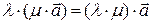
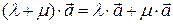
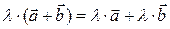
Эти свойства выполнены для любых чисел 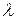, 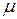и для любых векторов 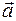и .