2015-06-28
722
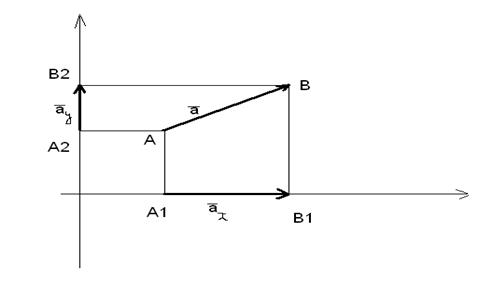
Рассмотрим плоскость, на которой введена декартова система координат для точек. Рассмотрим вектор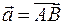 
на этой плоскости.
Обозначим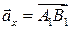 
(проекция 
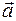на ось Ох) вектор, лежащий на оси абсцисс и соединяющий точки 
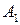и 
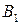, являющиеся, соответственно, проекциями точек 
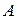и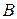 
на ось Ох. Пусть 
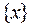- это координата вектора 
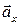на оси Ох. Аналогично определяется 
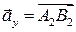(проекция 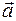на ось Оу) вектор, лежащий на оси ординат и соединяющий точки 
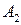и 
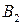, являющиеся, соответственно, проекциями точек 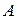и 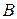на ось Оу. Пусть 
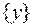- это координата вектора 
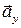на оси Оу. Координаты вектора 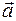- это упорядоченная пара чисел 
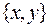, запись 
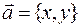означает, что вектор 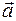имеет координаты .
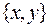Пусть известны координаты точек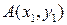 
и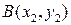 
, тогда абсциссы точек 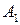и 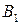совпадают, соответственно, с абсциссами точек 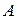и 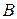, следовательно 
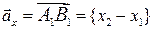. Рассуждая аналогично, получим, что 
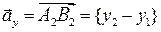. Отсюда вытекает формула для координат вектора 
:
.
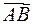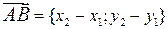Если разместить вектор 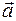началом в начале координат, то можно увидеть, что 
.
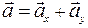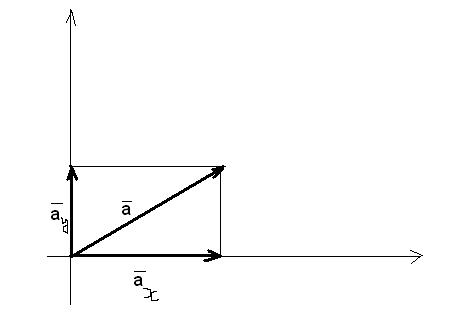
Вектор на плоскости выражает смещение, его координаты – числовые величины этого смещения вдоль осей координат.
Рассмотрим два вектора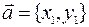 
, 
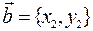и число 
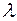, тогда
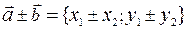, и
,
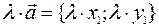то есть при сложении (вычитании) векторов их координаты складываются (вычитаются), при умножении вектора на число его координаты умножаются на это число.
Для доказательства этого достаточно представить векторы как суммы ,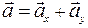 
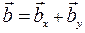. Тогда (для суммы) 
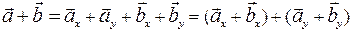. Очевидно, что 
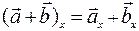, и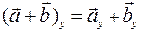 
, поэтому 
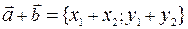. Аналогично доказываются остальные равенства (для разности и умножения на число).
