2015-06-28
527
Рассмотрим два вектора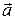 
и 
. Подберем векторы 
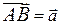и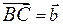 
. Тогда, по определению, вектор 
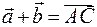, то есть нужно начало вектора приставить к концу вектора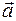 
, и вектор, соединяющий начало 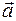и конец , будет равен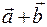 
.
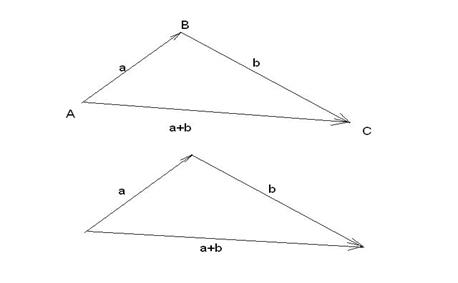
Нетрудно доказать корректность нашего определения, то есть, что результат не зависит от выбора начальной точки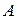 
, от которой мы начинаем свое построение.
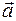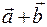Сложение векторов коммутативно, то есть для любых векторов и будут равны векторы и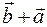 
. Проверяя это свойство, мы заодно получим «правило параллелограмма» сложения векторов применяемое в механике:
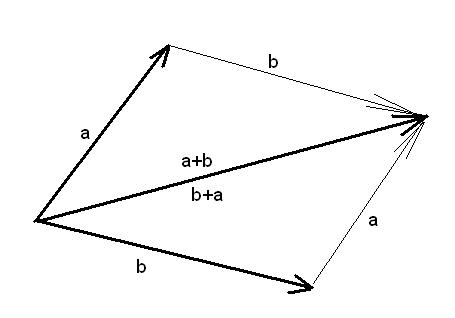
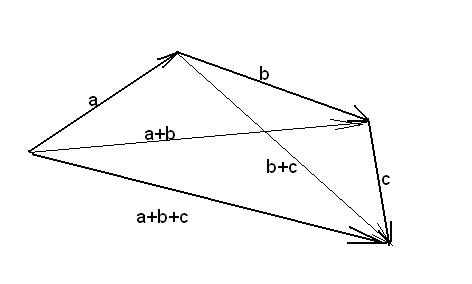
Сложение векторов также обладает свойством ассоциативности, то есть для любых векторов ,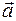 
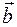и 
выполнено равенство: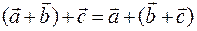 
, так что скобки можно вообще не ставить:
