Декартов базис

Рассмотрим плоскость с введенной на ней декартовой системой координат. Рассмотрим вектор 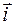, направленный по оси абсцисс и имеющий единичную длину (единичный вектор оси абсцисс). Рассмотрим также вектор 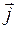, направленный по оси ординат и имеющий единичную длину (единичный вектор оси ординат).

Рассмотрим теперь любой вектор 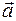на этой плоскости. Пусть известны координаты вектора 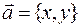. Тогда, легко понять, что

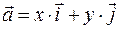
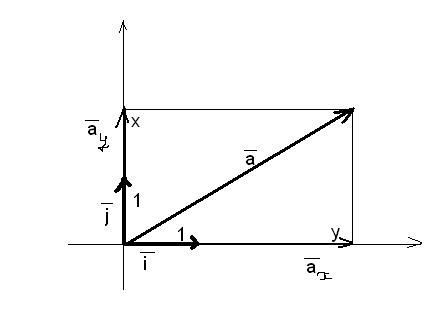
И обратно: если выполнено равенств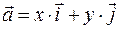о , то .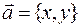

Выше (тема 3) мы рассматривали понятие базиса во множестве столбцов чисел: это такой набор столбцов этого множества, из которого можно получить с помощью линейных операций все остальные столбцы этого множества, при этом каждый столбец базиса не может быть получен из остальных столбцов базиса с помощью линейных операций (базис состоит из линейно независимых столбцов).

Аналогично, векторы 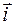, 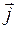образуют базис для всех векторов на плоскости. С помощью линейных операций можно получить из векторов 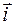, 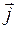любой вектор плоскости и, в то же время, нельзя выразить векторы 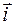и 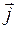друг через друга. Этот базис, состоящий из векторов 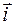, , 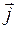называется

декартовым базисом для векторов на плоскости.

В пространстве, помимо векторов 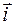и 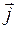, рассматривается единичный вектор оси аппликат – вектор 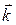. Также легко убедиться, что вектор 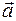имеет координаты 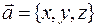тогда и только тогда, когда имеет место равенство 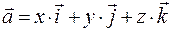. Набор векторов 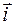, , 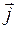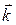образует декартов базис для векторов пространства.