2015-06-28
2234
Как известно, необходимым и достаточным условием коллинеарности двух ненулевых векторов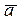 
и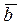 
является равенство:
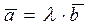, (1.6.4.1)
где скалярный множитель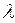 
>0, если векторы 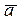и 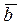имеют одинаковые направления и 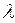<0 в противном случае.
Пусть заданны два вектора в координатной форме: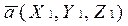 
и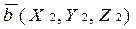 
.
В этом случае из равенства (1.6.4.1) следует, что
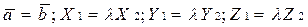, (1.6.4.2)
откуда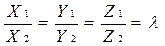 
(1.6.4.3)
Следовательно, если ненулевые векторы 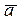и 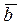коллинеарны, то и их одноименные координаты пропорциональны.
Необходимым и достаточным условием перпендикулярности векторов 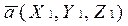и 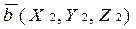является равенство:
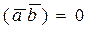(1.6.4.4)
или в координатной форме условие (1.6.4.4) имеет вид:
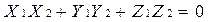(1.6.4.5)
