Скалярным произведением двух векторов 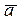 и
и 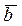 называется число,(обозначаемое
называется число,(обозначаемое 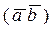 ) равное произведению длин векторов на косинус угла между ними:
) равное произведению длин векторов на косинус угла между ними:
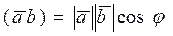 , (1.6.1)
, (1.6.1)
где 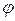 - угол между векторами
- угол между векторами 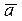 и
и 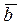 (рис.1.10).
(рис.1.10).
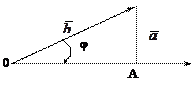
Рис. 1.10
1.6.1. Свойства скалярного произведения:
1). 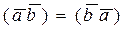
2). 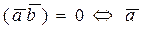 и
и 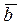 перпендикулярны; (или
перпендикулярны; (или 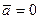 , или
, или 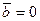 )
)
3). 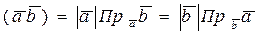
4). 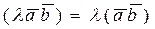 , где
, где 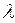 - число
- число
5). 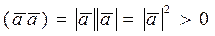 , если
, если 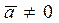
6). 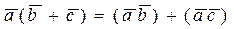
Докажем свойство 6. Имеем
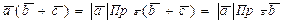
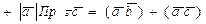
Замечание 1. Остальные свойства доказываются на основании определения.
Замечание 2. Свойства 1, 3, 4, 6 дают право при скалярном умножении векторных многочленов выполнять действия так же, как при умножении алгебраических многочленов.
Замечание 3. Скалярное умножение не распространяется на три и большее число векторов. Произведение, например, трех векторов 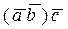 не является числом, оно будет вектором, коллинеарным вектору
не является числом, оно будет вектором, коллинеарным вектору 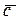 , который получается умножением вектора
, который получается умножением вектора 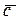 на число
на число 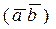 .
.
 2015-06-28
2015-06-28 382
382








