ОПРЕДЕЛЕНИЕ. Коэффициенты в разложении вектора по базису называются координатами этого вектора в данном базисе.
НАПРИМЕР.
1) Матрица 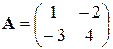 имеет в стандартном базисе
имеет в стандартном базисе 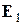 ,
, 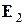 ,
, 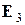 ,
, 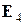 пространства
пространства 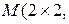 ℝ
ℝ 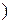 координаты
координаты 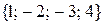 . Действительно,
. Действительно,
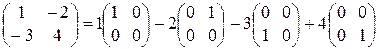 ,
,
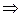
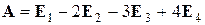 .
.
2) 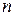 -мерный вектор
-мерный вектор 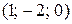 имеет в стандартном базисе пространства ℝ
имеет в стандартном базисе пространства ℝ 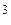 координаты
координаты 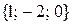
3) Многочлен 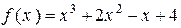 имеет в базисе
имеет в базисе 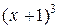 ,
, 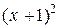 ,
, 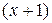 ,
, 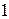 пространства ℝ
пространства ℝ 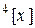 координаты
координаты 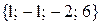
В линейном пространстве свободных векторов координаты вектора в декартовом прямоугольном базисе имеют простой геометрический смысл. Чтобы указать его, необходимо дать несколько определений.
ОПРЕДЕЛЕНИЕ. Прямую, на которой выбрано направление, называют осью.
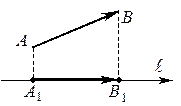 Пусть имеется некоторая ось
Пусть имеется некоторая ось 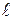 и вектор
и вектор 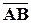 . Обозначим через
. Обозначим через 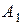 и
и 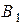 ортогональные проекции на ось
ортогональные проекции на ось 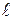 точек
точек 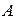 и
и 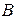 соответственно. Вектор
соответственно. Вектор 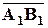 назовем векторной проекцией вектора
назовем векторной проекцией вектора 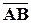 на ось
на ось 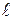 .
.
ОПРЕДЕЛЕНИЕ. Проекцией (ортогональной проекцией) вектора 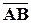 на ось
на ось 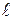 называется длина его векторной проекции
называется длина его векторной проекции 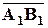 на эту ось, взятая со знаком плюс, если вектор
на эту ось, взятая со знаком плюс, если вектор 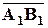 и ось
и ось 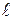 сонаправлены, и со знаком минус – если вектор
сонаправлены, и со знаком минус – если вектор 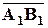 и ось
и ось 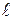 противоположно направлены.
противоположно направлены.
Проекцию вектора 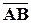 на ось
на ось 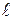 обозначают:
обозначают: 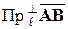 ,
, 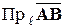 .
.
Справедливо следующее утверждение.
ТЕОРЕМА 7. Координаты вектора 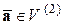
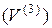 в декартовом прямоугольном базисе
в декартовом прямоугольном базисе 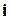 ,
, 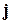 (
(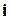 ,
, 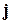 ,
, 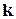 ) есть проекции этого вектора на соответствующие координатные оси.
) есть проекции этого вектора на соответствующие координатные оси.
ДОКАЗАТЕЛЬСТВО
Проведем доказательство для вектора 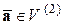 . Для вектора пространства
. Для вектора пространства 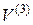 оно будет аналогичным.
оно будет аналогичным.
 Построим вектор
Построим вектор 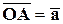 (вектор, с началом в точке
(вектор, с началом в точке 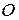 и концом в точке
и концом в точке 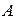 , называется радиус-вектором точки
, называется радиус-вектором точки 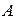 ). Обозначим через
). Обозначим через 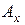 и
и 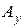 ортогональные проекции точки
ортогональные проекции точки 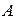 на ось
на ось 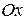 и
и 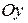 соответственно. Тогда
соответственно. Тогда
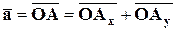
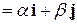 .
.
Так как 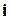 – вектор единичной длины, то
– вектор единичной длины, то 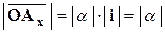 . Знак
. Знак 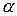 зависит от направления вектора
зависит от направления вектора 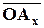 : если
: если 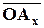 ⇈
⇈ 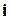 , то
, то 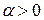 , если
, если 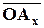 ⇅
⇅ 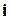 , то
, то 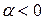 (см. определение произведения вектора на число). Но согласно определению проекции вектора на ось, это означает, что
(см. определение произведения вектора на число). Но согласно определению проекции вектора на ось, это означает, что 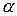 – проекция вектора
– проекция вектора 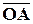 на ось, сонаправленную с вектором
на ось, сонаправленную с вектором 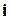 , т.е. на ось
, т.е. на ось 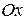 . Аналогично показывается, что
. Аналогично показывается, что 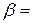
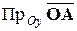 .
.
Координаты вектора – очень важная характеристика вектора любого линейного пространства. Знание координат векторов позволяет легко выполнять с ними линейные операции, так как справедлива следующая теорема.
ТЕОРЕМА 8. 1) Если вектор 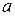 имеет в базисе
имеет в базисе 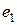 ,
, 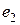 ,
,  ,
, 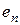 координаты
координаты 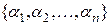 , а вектор
, а вектор 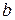 имеет в том же базисе координаты
имеет в том же базисе координаты 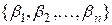 , то вектор
, то вектор 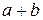 будет иметь в базисе
будет иметь в базисе 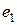 ,
, 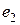 ,
,  ,
, 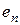 координаты
координаты 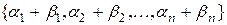 .
.
2) Если вектор 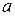 имеет в базисе
имеет в базисе 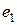 ,
, 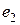 ,
,  ,
, 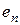 координаты
координаты 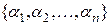 , то для любого числа
, то для любого числа 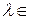 ℝ вектор
ℝ вектор 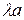 будет иметь в том же базисе координаты
будет иметь в том же базисе координаты 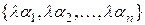 .
.
ДОКАЗАТЕЛЬСТВО
По условию 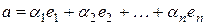 ,
, 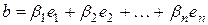 .
.
Тогда
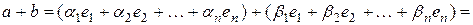
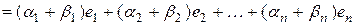
и 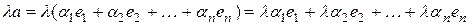 .
.
Из теоремы 8 вытекает справедливость следующего утверждения.
ТЕОРЕМА 9 (критерий коллинеарности свободных векторов в координатной форме). Векторы 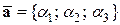 и
и 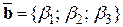 коллинеарны тогда и только тогда, когда их координаты –пропорциональны, т.е.
коллинеарны тогда и только тогда, когда их координаты –пропорциональны, т.е.
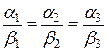
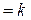 .
.
Причем, если коэффициент пропорциональности 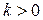 , то векторы
, то векторы 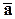 и
и 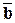 – сонаправлены, а если
– сонаправлены, а если 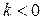 – то противоположно направлены
– то противоположно направлены
Координаты вектора определены в данном базисе единственным образом. Но в другом базисе вектор будет иметь другие координаты. Связь между координатами вектора в разных базисах дает следующая теорема.
ТЕОРЕМА 9. Пусть 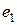 ,
, 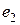 ,
,  ,
, 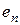 и
и 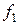 ,
, 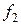 ,
,  ,
, 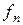 два базиса линейного пространства
два базиса линейного пространства 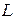 . Причем имеют место равенства:
. Причем имеют место равенства:
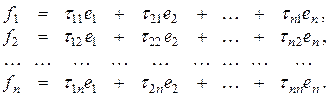
Если вектор 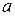 имеет в базисе
имеет в базисе 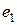 ,
, 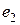 ,
,  ,
, 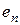 координаты
координаты 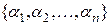 , а в базисе
, а в базисе 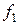 ,
, 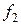 ,
,  ,
, 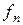 – координаты
– координаты 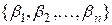 , то справедливо равенство
, то справедливо равенство 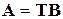 ,
,
где 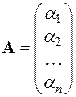 ,
, 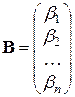 ,
, 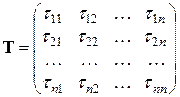 (матрицу
(матрицу 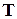 называют матрицей перехода от базиса
называют матрицей перехода от базиса 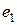 ,
, 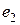 ,
,  ,
, 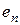 к базису
к базису 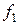 ,
, 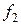 ,
,  ,
, 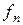 ).
).
ДОКАЗАТЕЛЬСТВО
По условию 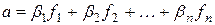 .
.
Расписывая векторы 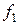 ,
, 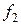 ,
,  ,
, 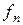 по базису
по базису 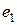 ,
, 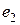 ,
,  ,
, 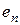 , получим:
, получим:
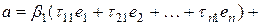
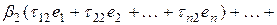
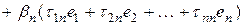 .
.
Раскроем скобки и перегруппируем слагаемые:
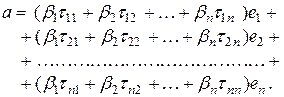 (1)
(1)
Так как по условию 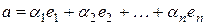 , то из (1) получаем:
, то из (1) получаем:
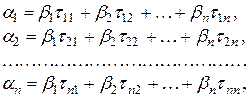
или в матричном виде 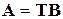 .
.
 2015-06-28
2015-06-28 2276
2276
