2015-06-28
2427
Понятие линейного пространства
(продолжение)
Напомним, что если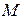 
– некоторое множество, элементы которого можно складывать и умножать на числа, то выражение 
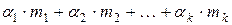(где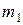 
, 
, 
, 
, 
, 
, , 
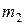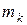
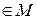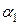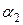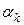– числа) называют линейной комбинацией элементов 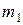, , 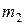, 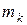с коэффициентами 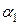, , 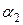, 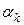. Если 
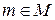и 
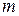является линейной комбинацией элементов 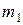, , 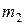, , 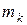т.е.
,
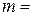
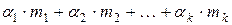то говорят, что 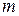линейно выражается через элементы , , , .
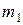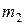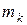Пусть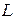 
– линейное пространство над ℝ(ℂ), 
, 
, , 
.
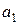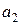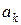
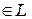ОПРЕДЕЛЕНИЕ. Говорят, что векторы 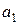, , 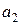, 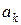линейно зависимы, если существуют числа 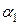, , 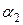, , 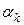не все равные нулю и такие, что линейная комбинация 
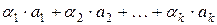равна нулевому элементу 
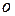линейного пространства .
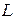Если же равенство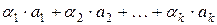 
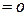возможно только при условии 
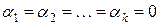, то векторы 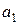, , 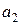, 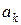называют линейно независимыми.
Справедливо следующее утверждение.
ЛЕММА 4. Векторы 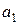, , 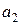, 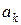линейно зависимы тогда и только тогда, когда хотя бы один из них линейно выражается через оставшиеся.
ДОКАЗАТЕЛЬСТВО
1) Необходимость.
Пусть векторы 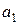, , 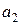, 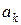– линейно зависимы. Тогда по определению существуют числа 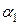, , 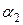, , 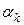не все равные нулю и такие, что
.
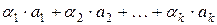
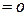Пусть, например,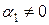 
. Тогда
,
.
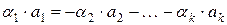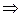
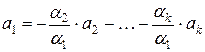2) Достаточность.
Пусть один из векторов 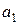, , 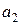, 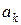линейно выражается через оставшиеся. Например, пусть
.
.
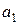
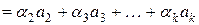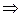
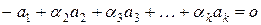Следовательно, векторы 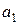, , 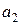, 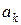– линейно зависимы.
Замечание. Часто в качестве определения линейно зависимых векторов берут формулировку леммы 4.
ПРИМЕРЫ.
1) Рассмотрим матрицы
, 
, 
, 
, 
.
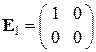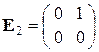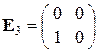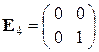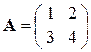Матрицы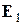 
, 
, 
, 
, 
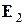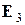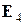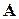– линейно зависимы, матрицы 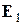, , 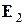, 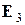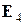– линейно независимы.
2) Многочлены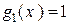 
, 
, 
, 
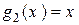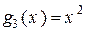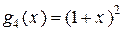– линейно зависимы, так как 
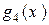является линейной комбинацией 
, 
, 
.
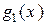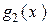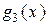Многочлены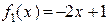 
, 
, 
, 
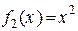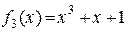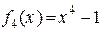– линейно независимы.
3) Пусть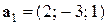 
, 
, 
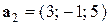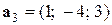. Выясним, является ли эта система векторов пространства ℝ 
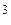линейно зависимой. Пусть 
.
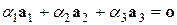Тогда имеем: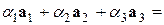 
.
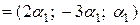
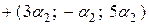
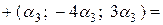
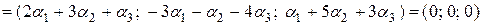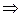
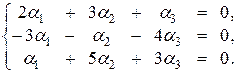
Таким образом, векторы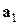 
, 
, 
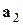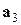будут линейно независимыми, если 
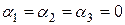– единственное решение системы. Согласно критерию единственности решения системы (см. §4) это будет иметь место, если 
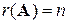, где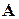 
– матрица системы, 
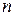– число неизвестных.
В нашем случае имеем: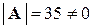 
,
.
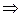
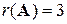Следовательно, система имеет только тривиальное решение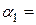 
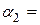
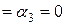, и, значит, векторы 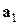, , 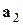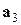– линейно независимые.
Теперь рассмотрим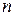 
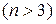произвольных векторов из ℝ :
, 
, , 
.
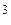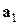
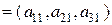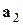
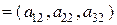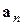
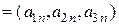Эти векторы всегда будут линейно зависимы. Действительно, рассмотрение линейной комбинации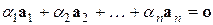 
приведет нас к системе уравнений
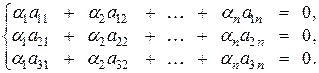
Так как 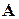– матрица размера 
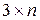и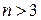 
, то ее ранг 
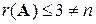. Следовательно, система будет иметь нетривиальные решения, и, значит равенство 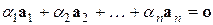возможно не только при нулевых коэффициентах.
Таким образом, мы можем утверждать, что в пространстве ℝ 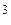линейно независимых векторов может быть не более трех.
ОПРЕДЕЛЕНИЕ. Максимальная линейно независимая система векторов линейного пространства называется базисом этого линейного пространства.
Иначе говоря, векторы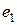 
, 
, , 
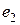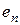
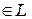образуют базис в линейном пространстве 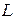если выполняются два условия:
1) 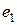, , 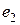, 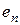– линейно независимы;
2) , , , , 
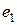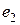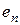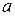– линейно зависимы для любого вектора 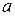из .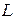
Очевидно, что в линейном пространстве существует не единственный базис (например, легко доказать, что если 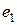, , 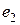, 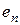образуют базис в линейном пространстве 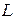и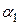 
, 
, , 
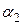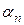– отличные от нуля действительные числа, то векторы 
, 
, , 
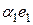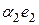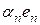тоже будут базисом). Но справедлива следующая теорема.
ТЕОРЕМА 5. Любые два базиса линейного пространства состоят из одного и того же числа векторов.
Если в линейном пространстве 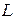существует базис из 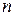векторов, то пространство называют конечномерным, а 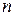называют размерностью линейного пространства (пишут: 
).
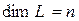Если в линейном пространстве 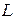для любого натурального 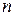можно найти линейно независимую систему векторов, то пространство называют бесконечномерным (пишут: 
).
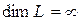ПРИМЕРЫ.
1) Линейное пространство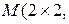 
ℝ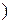 
матриц второго порядка с элементами из ℝ имеет размерность 
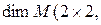ℝ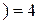 
. Его базисом будут, например, матрицы
, , , .
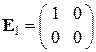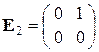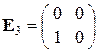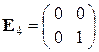Базис 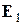, , 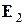, 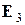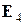в дальнейшем будем называть стандартным базисом пространства 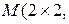ℝ .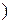
2) Множество свободных векторов плоскости 
является конечномерным линейным пространством. Его размерность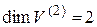 
. Базисом будут являться любые два неколлинеарных вектора.
Действительно, пусть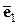 
, 
– неколлинеарные векторы на плоскости. Покажем, что они линейно независимы. Пусть
.
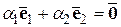Предположим, что хотя бы один из коэффициентов этой линейной комбинации отличен от нуля. Например,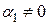 
. Тогда
,
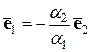и, значит, векторы 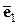и – коллинеарные. Следовательно, предположение неверно и линейная комбинация векторов 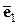, равна нулевому вектору только при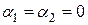 
, что и означает линейную независимость векторов , .
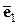Теперь покажем, что любой вектор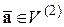 
можно представить в виде линейной комбинации векторов 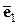и . Для этого построим векторы 
, 
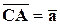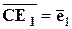и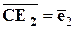 
. Через точку 
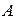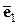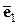проведем прямые параллельные векторам и . Точки пересечения этих прямых и прямых, на которых лежат векторы и , обозначим соответственно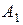 
и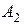 
. По правилу параллелограмма имеем:
.
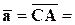
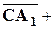
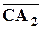Но векторы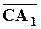 
и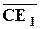 
коллинеарны, и, следовательно,
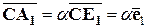
для некоторого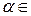 
ℝ. Аналогично
.
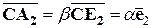Таким образом, получили
.
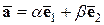3) Линейное пространство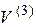 
свободных векторов пространства имеет размерность 
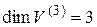. Легко доказать, что базисом в пространстве 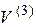являются любые три некомпланарных вектора.
Замечание. Хотя в качестве базиса на плоскости (в пространстве) можно взять любые два неколлинеарных (любые три некомпланарных) вектора, на практике предпочитают работать с декартовым прямоугольным базисом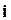 
, 
(, , 
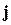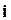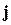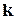). Это единичные векторы, которые сонаправлены координатным осям 
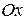и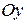 
соответственно (сонаправлены координатным осям 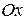, 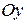и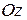 
соответственно).
4) Арифметическое линейное пространство ℝ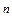 
тоже является конечномерным. Его размерность 
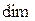ℝ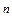 
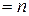. Базисом будут являться, например, векторы
, 
, , 
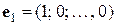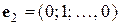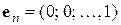
(будем называть его стандартным базисом пространства ℝ ).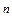
5) Пусть задана некоторая система линейных однородных уравнений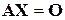 
, имеющая нетривиальные решения. Множество ℋ ее решений является конечномерным линейным пространством. Его базисом будет фундаментальная система решений, и, следовательно, 
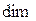ℋ 
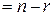, где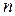 
– число неизвестных, 
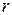– ранг матрицы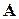
6) Линейное пространство ℝ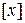 
многочленов с коэффициентами из ℝ является бесконечномерным. Легко проверить, что для любого натурального 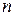многочлены
, 
, 
, , 
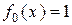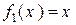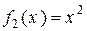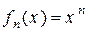
будут линейно независимы.
Роль базиса в линейном пространстве характеризует следующая теорема.
ТЕОРЕМА 6 (о базисе). Каждый вектор линейного пространства линейно выражается через любой его базис, причем единственным образом.
ДОКАЗАТЕЛЬСТВО
Пусть 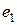, , 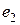, 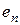– базис линейного пространства 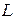и 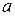– произвольный вектор из 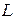. Тогда, по определению, 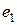, , 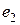, 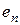– линейно независимы, а 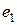, , 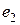, , 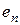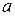– линейно зависимы. Следовательно, существуют числа , , , , 
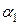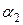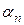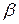не все равные нулю и такие, что линейная комбинация
.
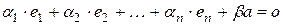Причем, коэффициент 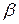не может быть равен нулю.
Действительно, если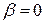 
, то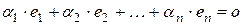 
, где коэффициенты 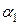, , 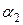, 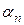не все равны нулю. Так как существует нулевая линейная комбинация элементов 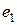, , 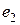, 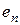с коэффициентами, среди которых есть ненулевые, то 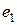, , 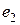, 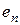– линейно зависимые. Но они по условию образуют базис, и, следовательно, линейно независимы.
Так как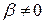 
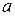, то линейно выражается через , , , :
,
.
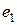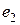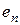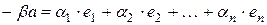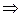
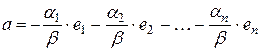Теперь докажем, что 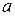линейно выражается через базис единственным образом. Предположим противное. Пусть
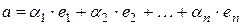
и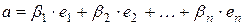 
,
причем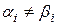 
хотя бы для одного 
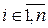. Пусть для определенности 
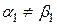. Тогда
,
.
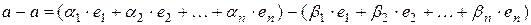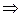
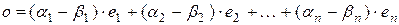Так как 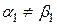, то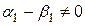 
. Таким образом, получили, что существует нулевая линейная комбинация векторов 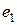, , 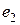, , 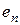среди коэффициентов которой есть ненулевые. Значит 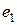, , 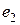, 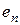– линейно зависимые. Но они по условию линейно независимы, так как образуют базис.
Следовательно, предположение неверное и вектор 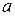разлагается по базису 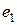, , 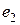, 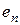единственным образом.
