Скалярное произведение векторов

ОПРЕДЕЛЕНИЕ. Скалярным произведением двух ненулевых векторов 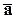и 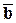называется число, равное произведению их модулей на косинус угла между ними, т.е. число

.

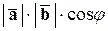Ес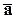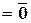ли или 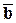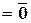, то скалярное произведение векторов 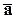и 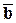полагают равным нулю.

Скалярное произведение векторов 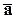и 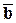обозначают 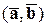или .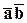

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

1) Скалярное произведение векторов коммутативно, т.е.

.

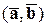
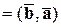Это свойство очевидно из определения.

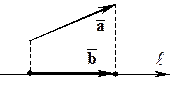2) Скалярное произведение ненулевых векторов 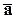и 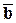равно произведению длины вектора 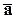на проекцию вектора 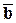на вектор 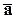(длины вектора 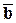на проекцию 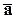на ).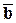

ОПРЕДЕЛЕНИЕ. Проекцией вектора 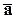на вектор 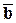называется проекция вектора 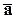на ось, определяемую вектором .

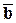Имеем: .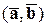

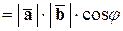Но , .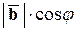

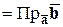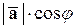
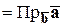Следовательно, ,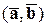

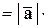
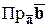и .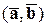

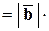
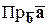3) Числовой множитель любого из двух векторов можно вынести за знак скалярного произведения. Т.е.

.

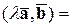
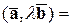
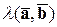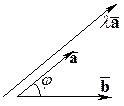Действительно, пусть 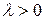. Тогда

,

.

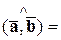
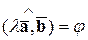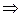
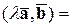
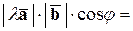
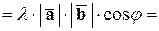
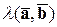Пусть 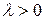. Тогда

, ,

.

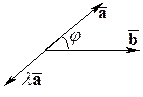
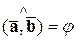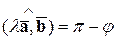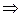
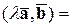
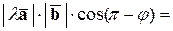
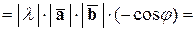
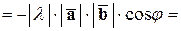
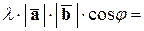
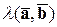4) Если один из векторов записан в виде суммы, то их скалярное произведение тоже можно записать в виде суммы. А именно:

,

.

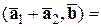
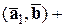
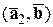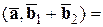
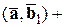
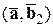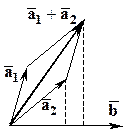Действительно,

.

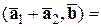
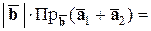
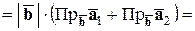
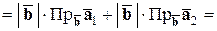
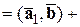
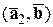5) Скалярное произведение вектора на себя (скалярный квадрат вектора) равно квадрату его длины. Т.е.

.

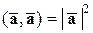Это свойство очевидно из определения.

6) Ненулевые векторы 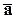и 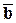перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (критерий перпендикулярности векторов).

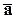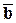Действительно, пусть векторы и перпендикулярны. Тогда

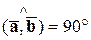и .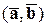

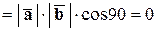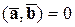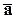
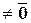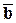
Обратно, пусть и , 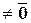. Тогда

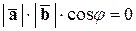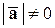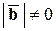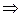
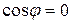и , ,

и .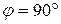

7) Если в декартовом прямоугольном базисе векторы 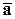и 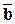имеют координаты: , ,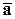

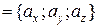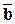
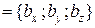то 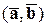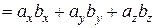. (1)

Формулу (1) называют выражением скалярного произведения через декартовы координаты векторов. Она легко выводится из свойств 4, 5, и 6.

8) Если под действием постоянной силы 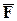точка перемещается по прямой из точки 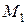в 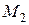, то работа силы 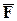будет равна

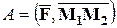
(физический смысл скалярного произведения).