Пусть на плоскости (в пространстве) задана декартова прямоугольная система координат. Выберем в пространстве 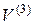 (
(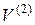 ) декартов прямоугольный базис
) декартов прямоугольный базис  ,
,  ,
,  (
(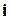 ,
,  ). Рассмотрим следующие задачи.
). Рассмотрим следующие задачи.
ЗАДАЧА 1. Найти координаты вектора 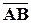 , если известны декартовы координаты начала и конца вектора.
, если известны декартовы координаты начала и конца вектора.
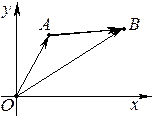 Пусть точки
Пусть точки  и
и 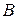 лежат в плоскости
лежат в плоскости 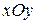 и имеют координаты
и имеют координаты 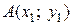 ,
, 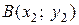 . Рассмотрим векторы
. Рассмотрим векторы 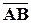 ,
, 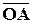 и
и 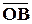 . Имеем:
. Имеем:
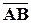
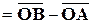 .
.
Но 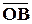
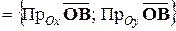
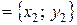 ,
,
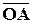
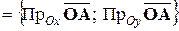
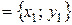 .
.
Следовательно, 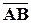
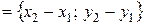 .
.
Аналогично получаем, что если 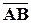
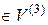 и
и 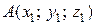 ,
, 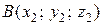 , то
, то
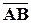
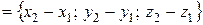 .
.
ЗАДАЧА 2. Найти длину вектора, если известны его координаты в декартовом прямоугольном базисе.
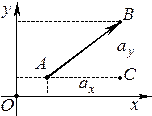 Пусть
Пусть 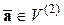 и
и 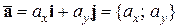 . Имеем:
. Имеем:
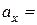
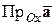 ,
, 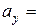
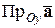 .
.
Рассмотрим треугольник 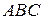 . Имеем:
. Имеем:
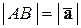 ,
, 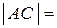
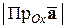
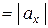 ,
, 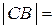
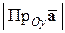
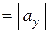 .
.
Следовательно, по теореме Пифагора,
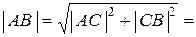
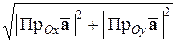 ,
,
Þ 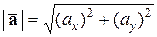 .
.
Аналогично получаем, что если 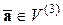 и
и
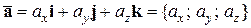 ,
,
то 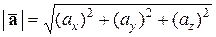 .
.
ЗАДАЧА 3. Известны координаты вектора. Найти координаты его орта.
ОПРЕДЕЛЕНИЕ. Ортом вектора 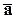 называется вектор
называется вектор 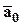 , сонаправленный с вектором
, сонаправленный с вектором 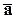 и имеющий единичную длину.
и имеющий единичную длину.
Пусть 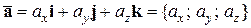 . Так как векторы
. Так как векторы 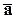 и
и 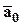 сонаправленны, то существует
сонаправленны, то существует 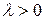 такое, что
такое, что 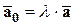 . Следовательно
. Следовательно
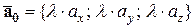 .
.
Найдем 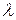 . Имеем:
. Имеем:
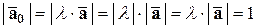 ,
,
Þ 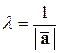 .
.
Таким образом, получаем:
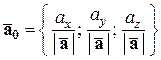 .
.
Координаты орта вектора имеют очень простой геометрический смысл. Обозначим через 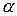 ,
, 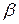 и
и 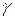 углы, которые вектор
углы, которые вектор 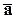 образует с координатными осями
образует с координатными осями  ,
, 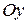 и
и 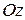 соответственно.
соответственно. 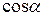 ,
, 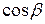 ,
, 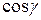 называются направляющими косинусами вектора
называются направляющими косинусами вектора 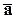 . Выразим направляющие косинусы вектора через его координаты. Имеем:
. Выразим направляющие косинусы вектора через его координаты. Имеем:
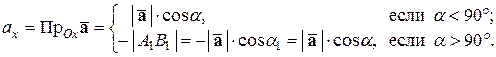
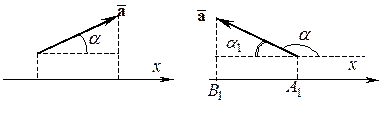 |
Аналогично находим:
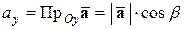 ,
, 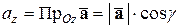 .
.
Следовательно,
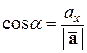 ,
, 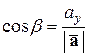 ,
, 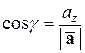 .
.
Таким образом, получили, что координаты орта вектора 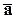 являются его направляющими косинусами.
являются его направляющими косинусами.
Замечание. Так как 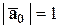 и
и 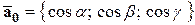 , то
, то
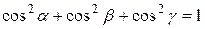 .
.
Это равенство называют основным тождеством для направляющих косинусов вектора.
ЗАДАЧА 4. Известны координаты концов отрезка. Найти координаты точки, которая делит отрезок в заданном отношении.
ОПРЕДЕЛЕНИЕ. Говорят, что точка 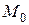 делит отрезок
делит отрезок 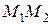 в отношении
в отношении 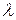
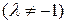 если
если 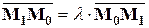 .
.
Если 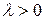 , то точка
, то точка 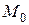 лежит между точками
лежит между точками 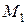 и
и 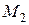 . В этом случае говорят, что точка
. В этом случае говорят, что точка 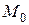 делит отрезок
делит отрезок 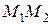 во внутреннем отношении.
во внутреннем отношении.
Если 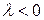 , то точка
, то точка 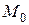 лежит на продолжении отрезка
лежит на продолжении отрезка 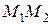 и говорят, что точка
и говорят, что точка 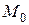 делит отрезок
делит отрезок 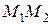 во внешнем отношении.
во внешнем отношении.
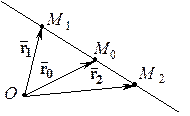 Пусть
Пусть 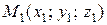 ,
, 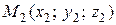 и
и 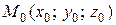 . Обозначим через
. Обозначим через 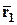 ,
, 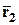 ,
, 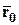 – радиус-векторы точек
– радиус-векторы точек 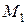 ,
, 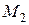 и
и 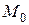 соответственно. Тогда
соответственно. Тогда
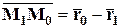 ,
, 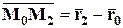 .
.
Так как 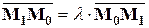 , то
, то
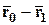
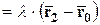 ,
,
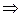
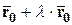
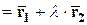 ,
,
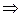
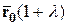
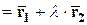 ,
,
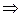
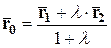 (1)
(1)
или в координатной форме:
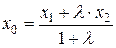 ,
, 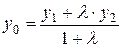 ,
, 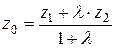 . (2)
. (2)
В частности, если 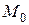 – середина отрезка
– середина отрезка 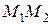 , то
, то
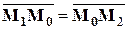 ,
,
т.е. 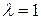 и формулы (1) и (2) примут вид:
и формулы (1) и (2) примут вид:
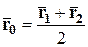
и 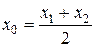 ,
, 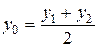 ,
, 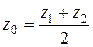 .
.
Замечание. Если точка 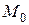 лежит между точками
лежит между точками 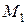 и
и 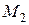 , то обычно говорят, что
, то обычно говорят, что 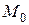 делит отрезок
делит отрезок 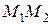 в отношении
в отношении 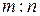 . В этом случае
. В этом случае 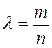 , а формулы (1) и (2) можно переписать в виде:
, а формулы (1) и (2) можно переписать в виде:
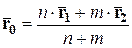
и 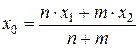 ,
, 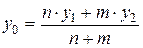 ,
, 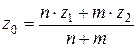 .
.
§9. нелинейные операции на множестве
векторов
 2015-06-28
2015-06-28 1865
1865








