Решение. Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС

Обозначим медианы треугольника АВС через ВЕ, СF и обозначим векторы, идущие вдоль сторон треугольника АВС, через а, в, с:

ВС = а, СА = в, АВ = с

(рис.8). Тогда

АD = АВ + ВD = АВ + 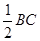= с +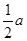

аналогично определяются и другие медианы:

ВЕ = а + 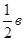, СF = в +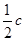

Так как, в силу условия замкнутости

ВС + СА + АВ = а + в + с = 0,

то мы имеем:

АD + ВЕ + СF = (с + 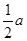) + (а + 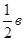) + (в + 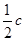) = 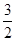(а + в + с) = 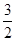х 0 = 0.

Следовательно, отложив от точки В, вектор В₁С₁ = ВЕ и от точки С₁ – вектор С₁D₁ = СF, мы получим.

А₁В₁ + В₁С₁ + С₁D₁ = АD + ВЕ + СF = 0.

А это значит (в силу условия замкнутости), что ломаная А₁В₁С₁D₁ является замкнутой, т.е. точка D₁ совпадает с А₁.

Таким образом, мы получаем треугольник А₁В₁С₁ (рис.9), стороны которого равны и параллельны медианам АD, ВЕ, СF исходного треугольника.