2015-06-28
787
Определение 1. Пусть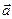 
и 
– ненулевые векторы на плоскости, тогда 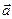и называются коллинеарными, если их носители параллельны или совпадают.
Теорема1. Векторы 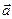и коллинеарные тогда и только тогда, когда существует такое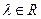 
, что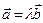 
.
Доказательство:
Необходимость. Пусть вектора 
и коллинеарные. Тогда по определению они лежат на одной или параллельных прямых. С помощью параллельного переноса совместим начала векторов 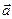и . Тогда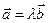 
, где
| рис. 2.13 |
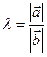, если 
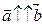(сонаправлены), или 
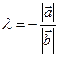, если 
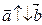; (котранаправлены). (Рис. 2.13).
Достаточность. Пусть 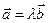. Тогда по определению произведения вектора на числа получаем коллинеарность векторов 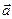и . ■
Определение 2. Базисом на плоскости будем называть всякую упорядоченную пару неколлинеарных векторов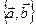 
. Совокупность фиксированной точки 
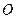плоскости и произвольного базиса 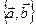на плоскости, приведенного к этой точке, называется аффинной системой координат (АСК) 
.
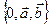Теорема2. Пусть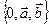 
некоторая АСК на плоскости. Тогда любой вектор 
этой плоскости можно представить в виде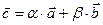 
, 
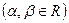и при том единственным образом.
Доказательство:
Покажем существование разложения вектора . Совместим начало вектора с точкой .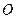
Проведём через конец вектора прямые, параллельные 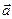и . Тогда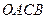 
– параллелограмм. Отсюда 
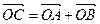. Но векторы 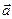и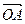 
коллинеарные, значит 
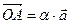. Аналогично, векторы 
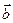и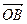 
коллинеарные, значит 
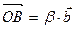. Тогда 
.
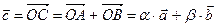Теперь докажем единственность разложения.
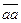. Пусть существует два разложения по базису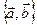 
: 
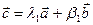и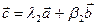 
такие, что 
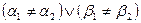. Тогда 
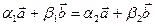или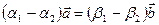 
.
Если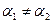 
, то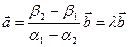 
, что означает коллинеарность векторов 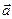и и противоречит условию.
Аналогично, если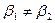 
, то получим коллинеарность 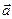и , что противоречит условию. Таким образом,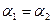 
, 
. ■
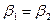Такое представление вектора называется разложением по базису 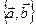, а числа 
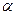и 
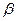называются координатами в АСК 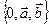. Вектор в этом случае можно записать так: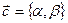 
.
Замечание. Если векторы базиса выбрать взаимно перпендикулярными и имеющими единичную длину, то такая АСК на плоскости носит названиедекартовой прямоугольной системой координат (ДПСК).Базисные вектора, входящие в ДПСК обозначают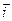 
и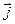 
(кратчайший поворот против часовой стрелки от 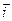к ).
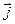На плоскости существуют и другие системы координат. Задавая на плоскости некоторую АСК, мы устанавливаем взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел.
