Для того чтобы система векторов 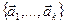 была линейно зависима, необходимо и достаточно, чтобы существовали действительные числа
была линейно зависима, необходимо и достаточно, чтобы существовали действительные числа 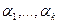 , не равные нулю одновременно, такие, что
, не равные нулю одновременно, такие, что 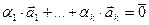 . (1)
. (1)
(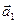 ,…,
,…, 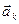 – система линейно зависима)
– система линейно зависима) 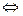
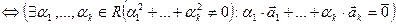 .
.
Доказательство:
Необходимость. Пусть система 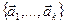 линейно зависима. Тогда по определению хотя бы один из векторов системы, например,
линейно зависима. Тогда по определению хотя бы один из векторов системы, например, 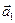 , можно представить в виде линейной комбинации остальных векторов:
, можно представить в виде линейной комбинации остальных векторов: 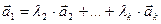 . Прибавим к обеим частям равенства –
. Прибавим к обеим частям равенства – 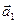 , получим:
, получим: 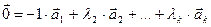 .
.
Положим 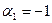 ,
, 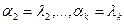 , не все
, не все 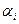 равны нулю одновременно, причем выполняется равенство (1).
равны нулю одновременно, причем выполняется равенство (1).
Достаточность. Пусть существуют 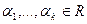 ,
, 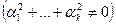 такие, что
такие, что 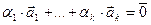 . Среди чисел
. Среди чисел 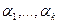 , по крайней мере, одно не равно нулю, например,
, по крайней мере, одно не равно нулю, например, 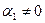 . Тогда получим
. Тогда получим 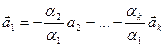 , что означает по определению линейную зависимость векторов
, что означает по определению линейную зависимость векторов 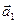 ,…,
,…, 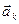 . ■
. ■
 2015-06-28
2015-06-28 365
365








